Materials
今回は3次元Schrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \Psi (t, x, y, z) = H \Psi (t, x), \qquad H = - \frac{\hbar^2}{2 m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) + V (x, y, z), \] について学ぶ。 1次元の場合と同様、\( \Psi (t, x, y, z) = \psi (x, y, z) \varphi (t)\) 型の解を考えて、時間に依存しないSchrödinger方程式 \[ H \psi (x, y, z) = E \psi (x, y, z), \] に帰着できる。 特に球対称なポテンシャル \( V (x, y, z) = V (r) \) に対しては、動径方向 \( r \) と角度方向 \( \theta, \phi \) に分けて \( \psi (x, y, z) = R (r) Y (\theta, \phi) \) という形の解を考えると見通しが良く、それぞれについての方程式が \[ \frac{1}{R (r)} \frac{d}{d r} \left( r^2 \frac{d}{d r} R (r) \right) - \frac{2 m r^2}{\hbar^2} \left( V (r) - E \right) = l (l + 1), \] \[ \frac{1}{Y (\theta, \phi)} \left[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} Y (\theta, \phi) \right) + \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} Y (\theta, \phi) \right] = - l (l + 1), \] と分離する。 極座標の取り方は下図の通りである。
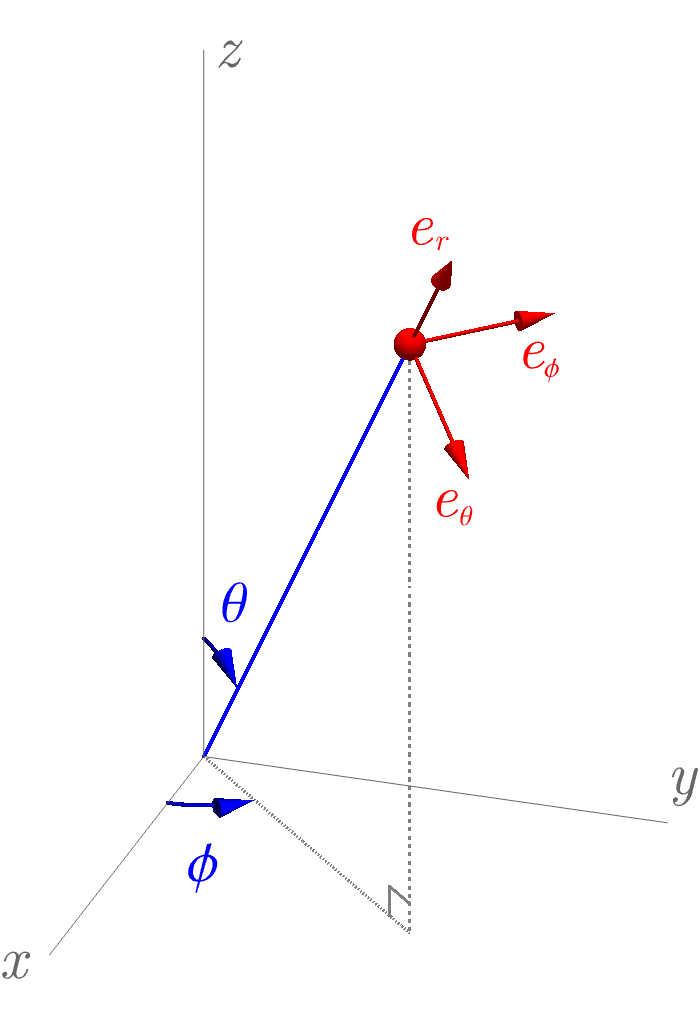
さて、分離した方程式のうち後者の解はポテンシャル \( V (r) \) の関数形によらず決まるため重要で、球面調和関数と呼ばれる関数 \[ Y_{l m} (\theta, \phi) = \sqrt{\frac{(2 l + 1)!}{4 \pi} \frac{(l - m)!}{(l + m)!}} \, e^{i m \phi} \, P_l^m (\cos \theta), \] を用いて \( Y (\theta, \phi) = Y_{l m} (\theta, \phi) \) となることが知られている。 それぞれの \( (l, m) \) について \( Y_{l m} (\theta, \phi) \) の関数形がどうなるか見てみよう。 下図では、各方向 \( (\theta, \phi) \) について絶対値 \( |Y_{l m} (\theta, \phi)| \) が動径 \( r \) で示され、位相 \( \arg (Y_{l m} (\theta, \phi)) \) が色で示されている。 いくつかの特徴に気付くだろうか。
(1) \( \phi \) 方向に1周すると位相が \( 2 \pi |m| \) だけ回る。 これは \( Y_{l m} (\theta, \phi) \propto e^{i m \phi} \) の依存性から来る振る舞いである。
(2) \( \theta \) 方向に \( 0 \) から \( \pi \) まで動くと、絶対値 \( |Y_{l m} (\theta, \phi)| \) が \( l - |m| \) 回だけ \( 0 \) を横切る。 これは \( Y_{l m} (\theta, \phi) \propto P_l^m (\cos \theta) \) の依存性から来る振る舞いである。
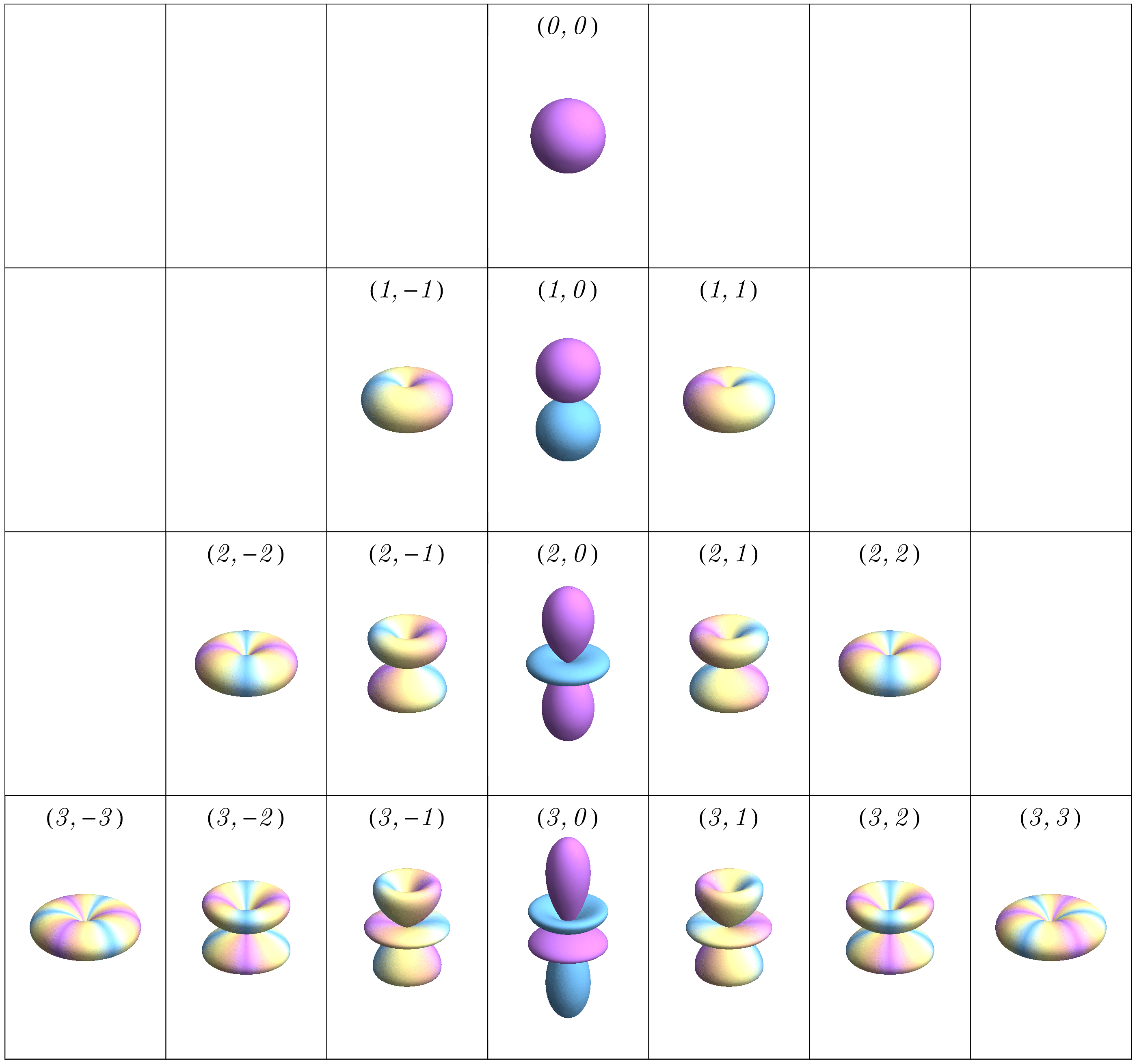
ちなみに、\( (l, m) = (50, 25) \) に対する球面調和関数は以下のようになる。
