Materials
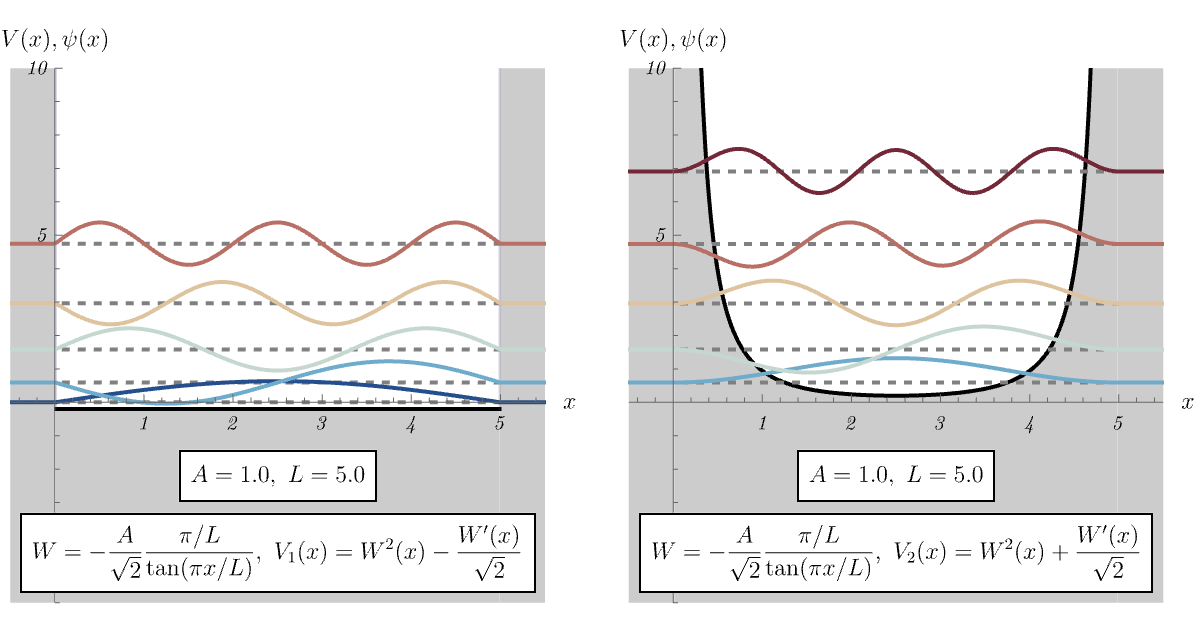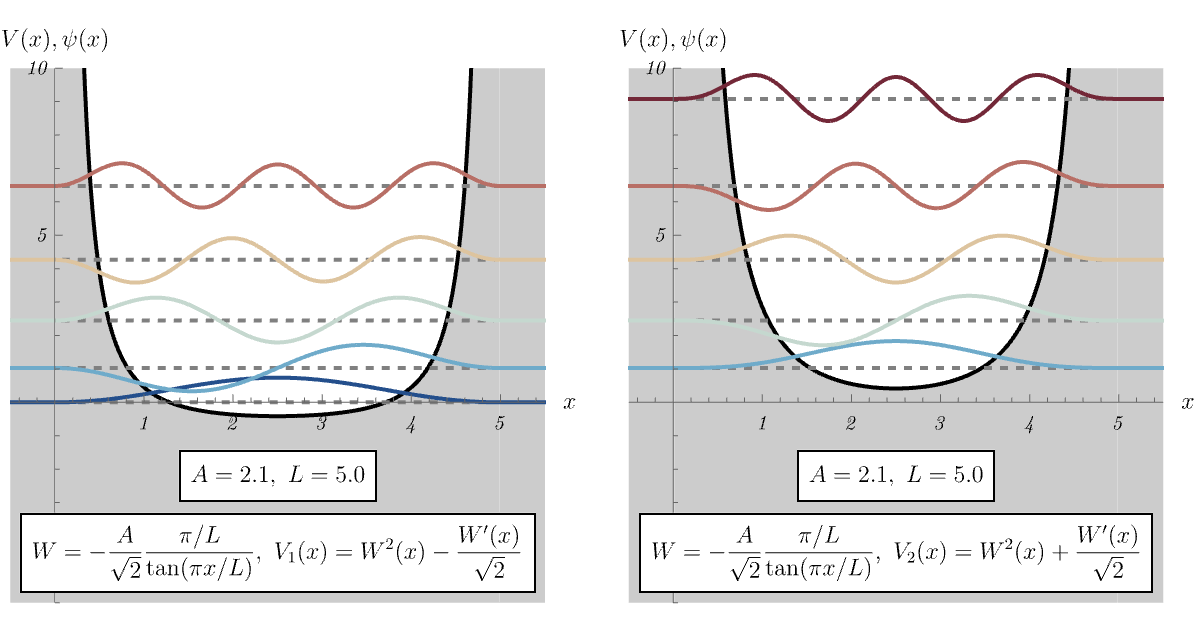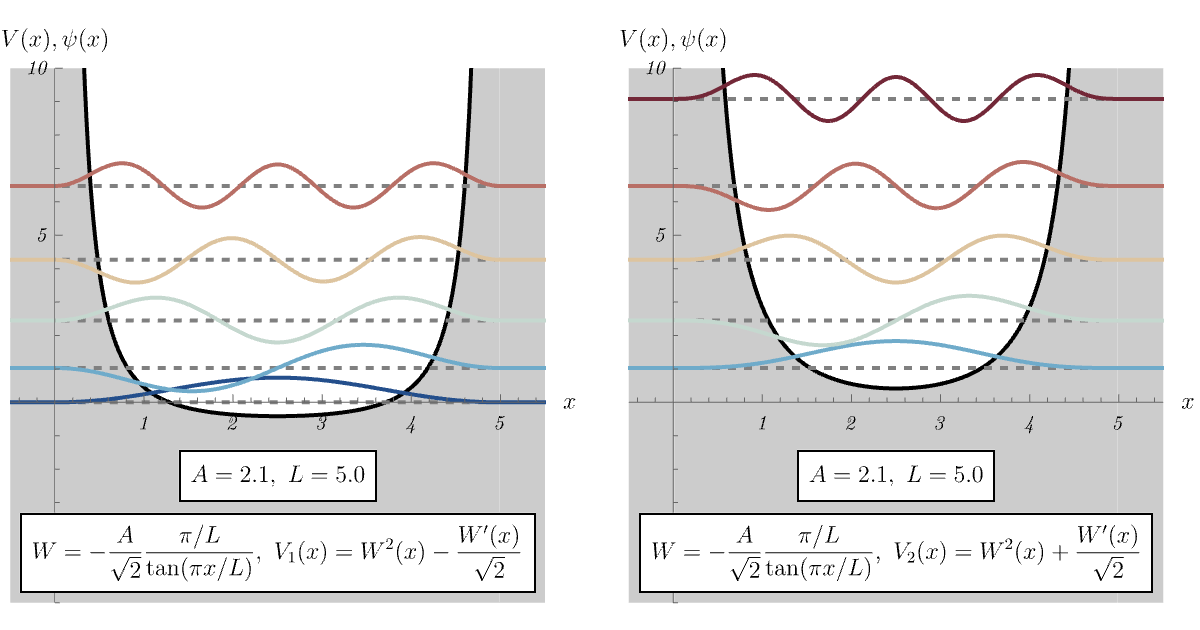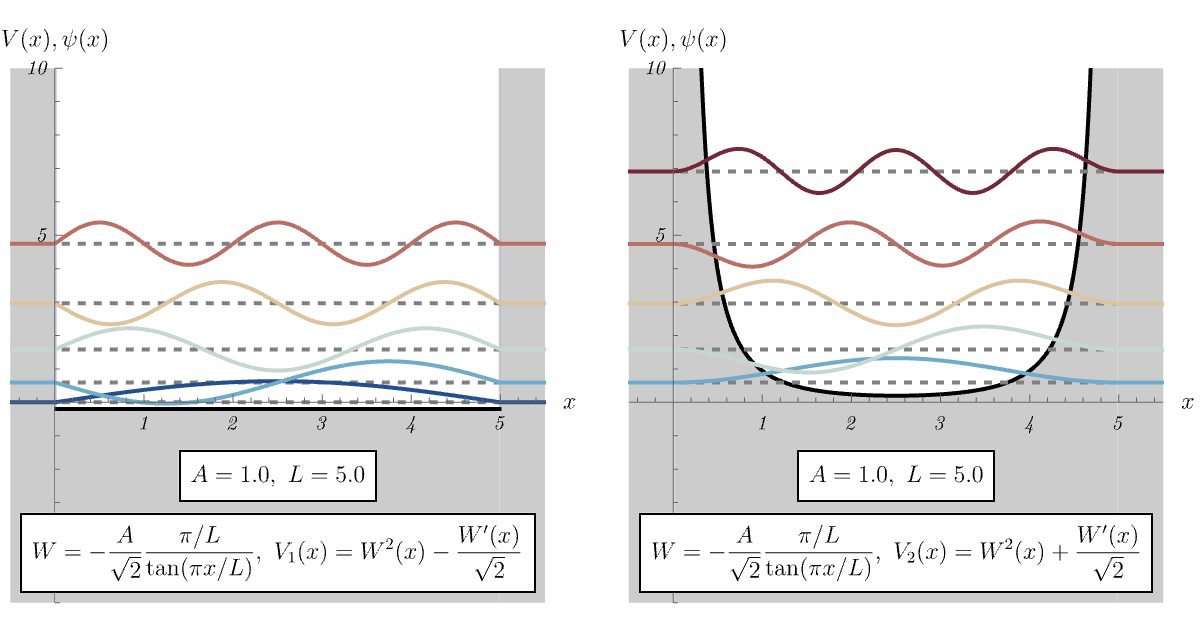
今回はちょっと脱線して、超対称量子力学 (supersymmetric quantum mechanics = SUSY QM) を見てみよう。 演算子 \[ \hat{A} = \frac{i}{\sqrt{2 m}} \hat{p} + W (\hat{x}), \qquad \hat{A}^\dagger = - \frac{i}{\sqrt{2 m}} \hat{p} + W (\hat{x}), \qquad\] を考える。 ここに現れる \( W (\hat{x}) \) はsuperpotentialと呼ばれ、\( (W (\hat{x}))^\dagger = W (\hat{x}) \) を満たしている。 \( \hat{A}, \hat{A}^\dagger\) を用いて2種類のHamiltonianを作ってみる \[ \hat{H}_1 = \hat{A}^\dagger \hat{A} = \frac{\hat{p}^2}{2 m} + V_1 (\hat{x}), \qquad V_1 (\hat{x}) = W^2 (\hat{x}) - \frac{\hbar}{\sqrt{2 m}} W' (\hat{x}), \] \[ \hat{H}_2 = \hat{A} \hat{A}^\dagger = \frac{\hat{p}^2}{2 m} + V_2 (\hat{x}), \qquad V_2 (\hat{x}) = W^2 (\hat{x}) + \frac{\hbar}{\sqrt{2 m}} W' (\hat{x}). \] すると、\( \hat{H}_1 \) と \( \hat{H}_2 \) は異なるポテンシャルを持つにも関わらず、(ほとんど) 同じエネルギー準位を持つ。
トリックは以下の通りである。 \( \ket{\psi_n^{(1)}} \) が \( \hat{H}_1 \) の固有値 \(E_n^{(1)} \) の固有状態であるとすると、\( \hat{A} \ket{\psi_n^{(1)}} \) は \( \hat{H}_2 \) の同じ固有値の固有状態になっている \[ \hat{H}_1 \ket{\psi_n^{(1)}} = E_n^{(1)} \ket{\psi_n^{(1)}} \qquad \implies \qquad \hat{H}_2 (\hat{A} \ket{\psi_n^{(1)}}) = E_n^{(1)} (\hat{A} \ket{\psi_n^{(1)}}). \] 同様に、\( \ket{\psi_n^{(2)}} \) が \( \hat{H}_2 \) の固有値 \(E_n^{(2)} \) の固有状態であるとすると、\( \hat{A}^\dagger \ket{\psi_n^{(2)}} \) は \( \hat{H}_1 \) の同じ固有値の固有状態になっている \[ \hat{H}_2 \ket{\psi_n^{(2)}} = E_n^{(2)} \ket{\psi_n^{(2)}} \qquad \implies \qquad \hat{H}_1 (\hat{A}^\dagger \ket{\psi_n^{(2)}}) = E_n^{(2)} (\hat{A}^\dagger \ket{\psi_n^{(2)}}). \] 「ほとんど」と言ったのには理由がある。 まず、\( \hat{H}_1 \) の基底状態を略記して \( \ket{\psi_0} \) としよう。 仮に \( \hat{A} \ket{\psi_0'} = 0 \) となる状態 \( \ket{\psi_0'} \) が存在すれば、それこそが \( \ket{\psi_0} \) となる。 なぜなら、\( \hat{H}_1 \) の任意の固有状態 \( \ket{\psi} \) に対して固有値 \( E^{(1)} \) は \( E^{(1)} = E^{(1)} \braket{\psi | \psi} = \bra{\psi} \hat{H}_1 \ket{\psi} = \left| \hat{A} \ket{\psi} \right|^2 \geq 0 \) である一方、 \( \hat{A} \ket{\psi_0'} = 0 \) となる状態 \( \ket{\psi_0'} \) は \( \hat{H}_1 \ket{\psi_0'} = \hat{A}^\dagger \hat{A} \ket{\psi_0'} = 0 \ket{\psi_0'} \) より \( \hat{H}_1 \) の固有値の最低値 \( 0 \) を実現しているからである。 この場合、対応する \( \hat{H}_2 \) の固有ベクトル \( \hat{A} \ket{\psi_0} \) は存在しなくなってしまうため、\( \hat{H}_1 \) の最低エネルギー準位に対応する\( \hat{H}_2 \) のエネルギー準位が存在しなくなる。 以下、例を見てみよう。
8-1. 調和振動子
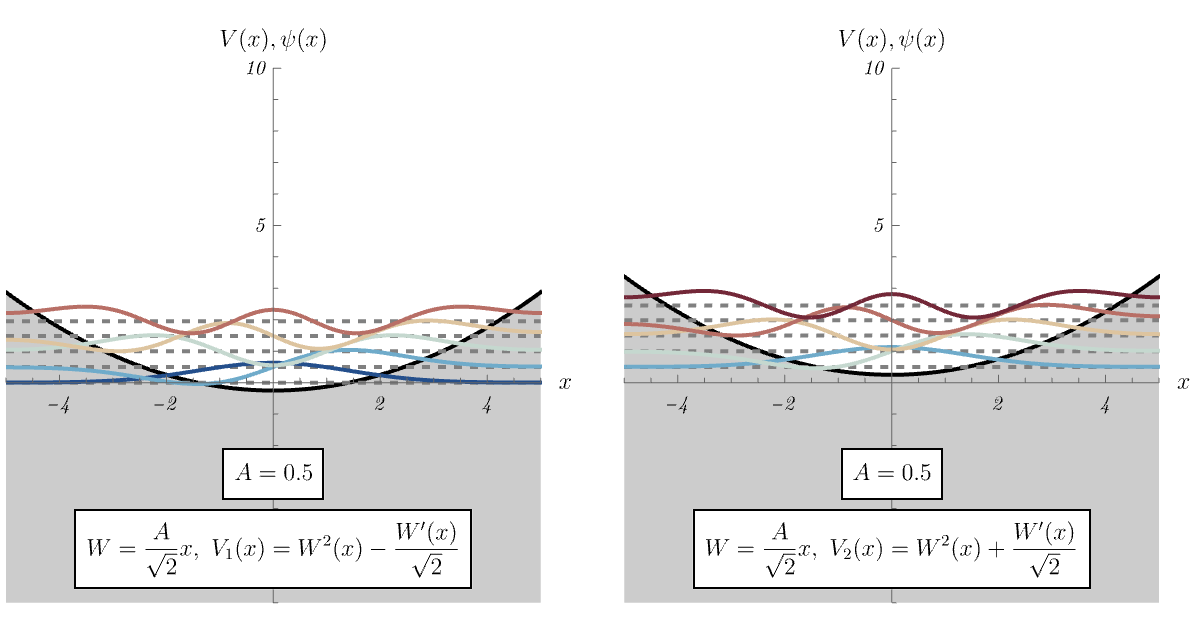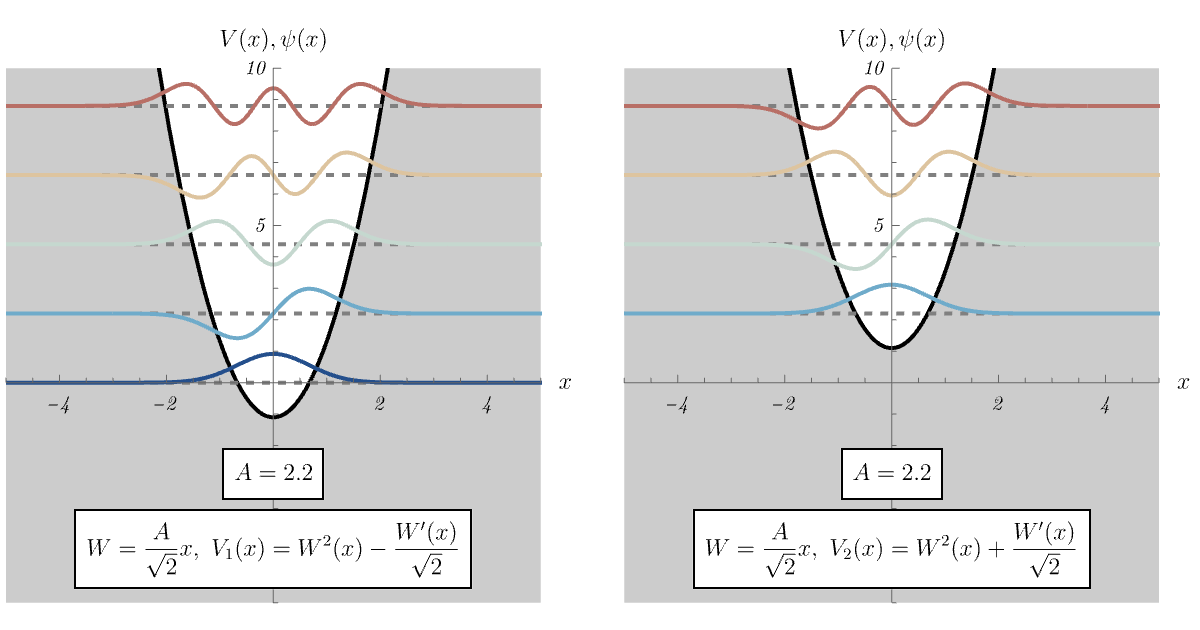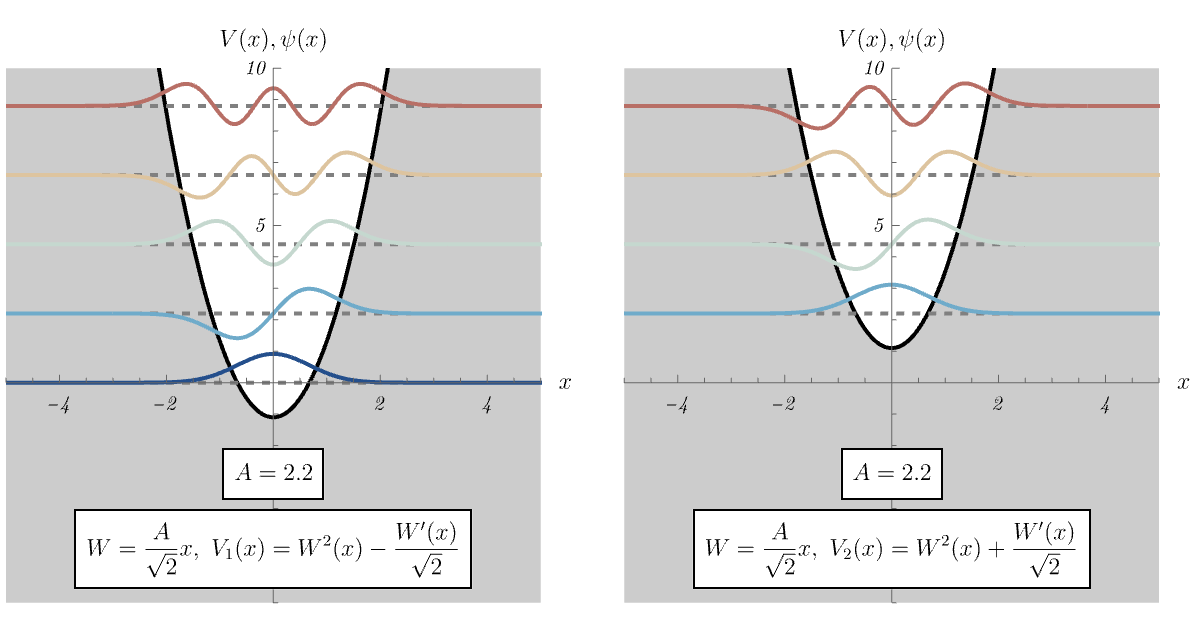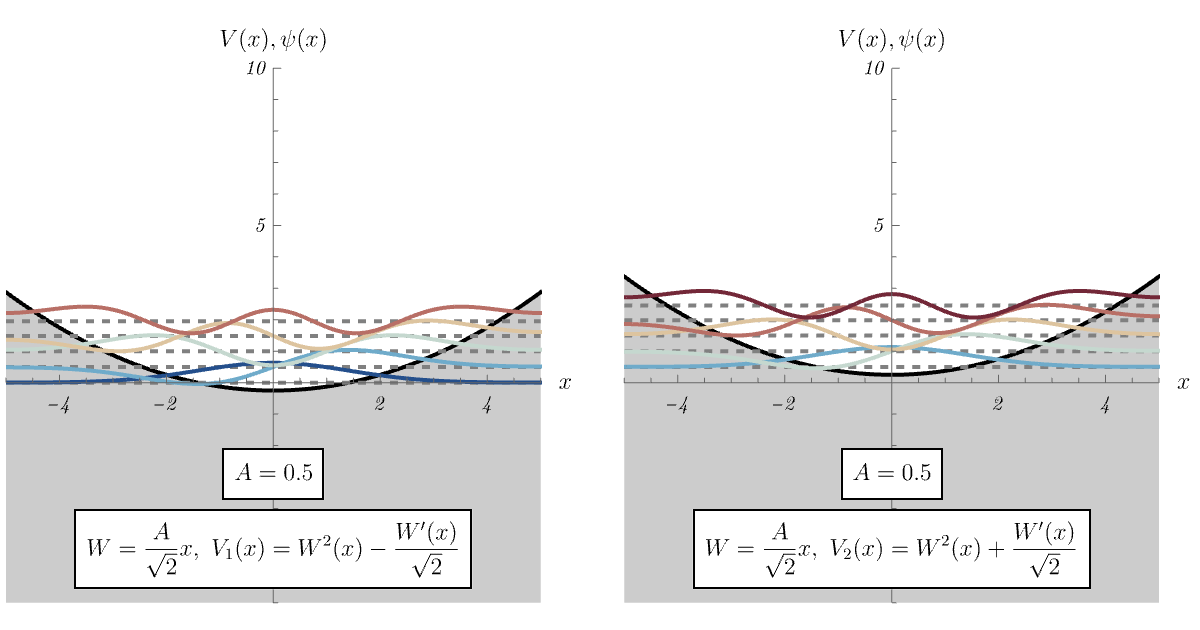
8-2. 無限井戸型ポテンシャル
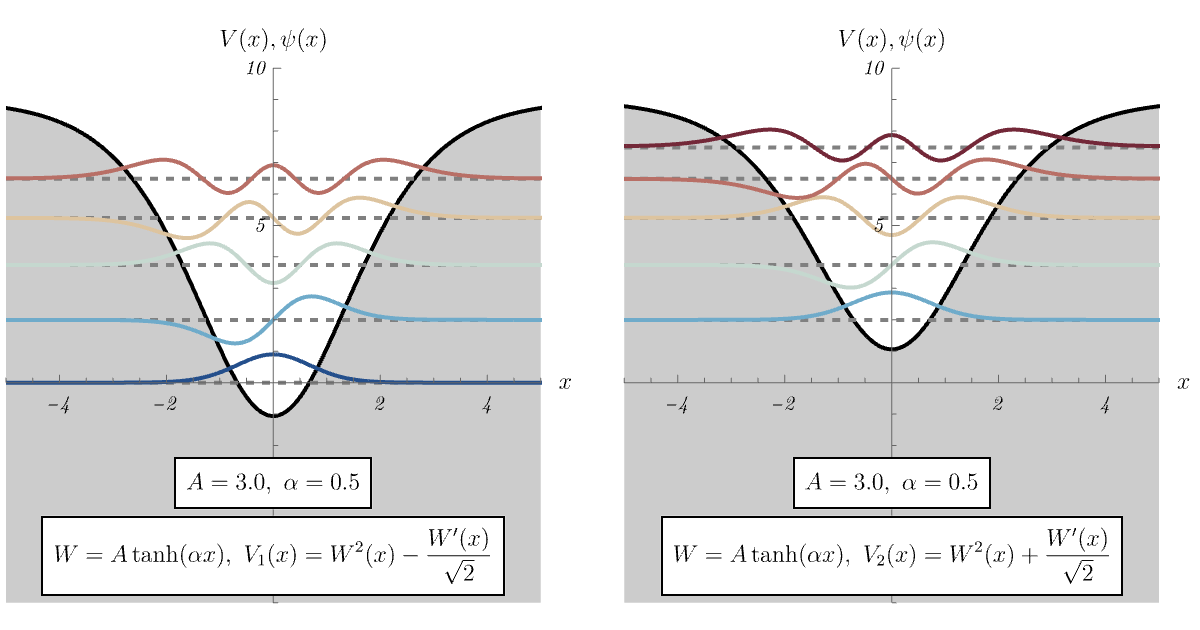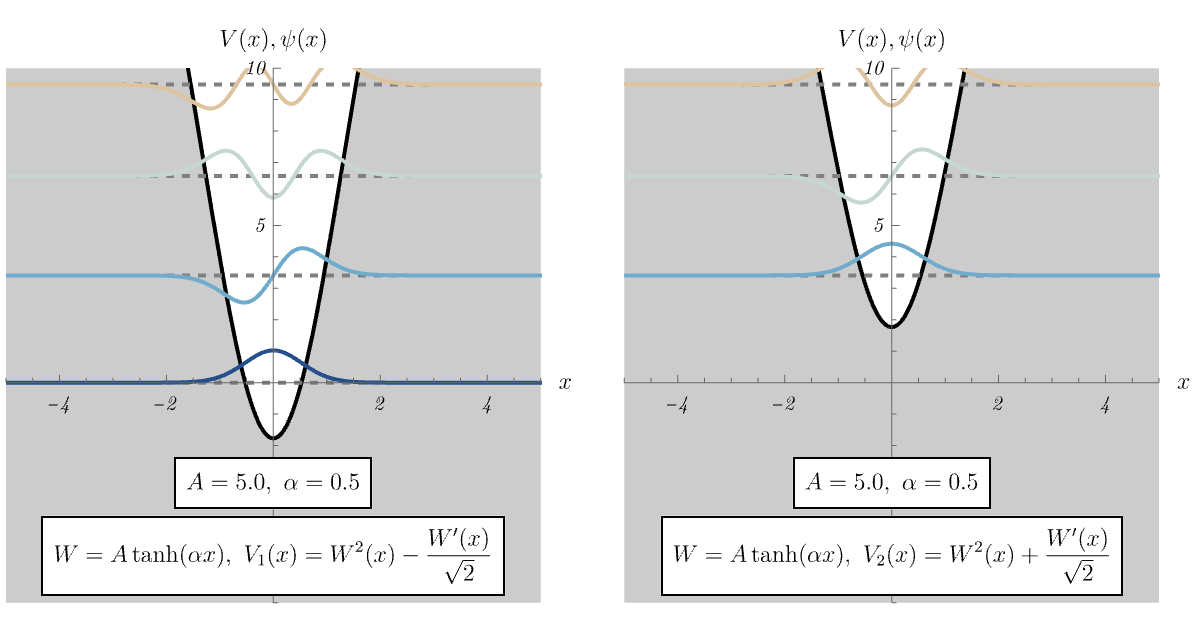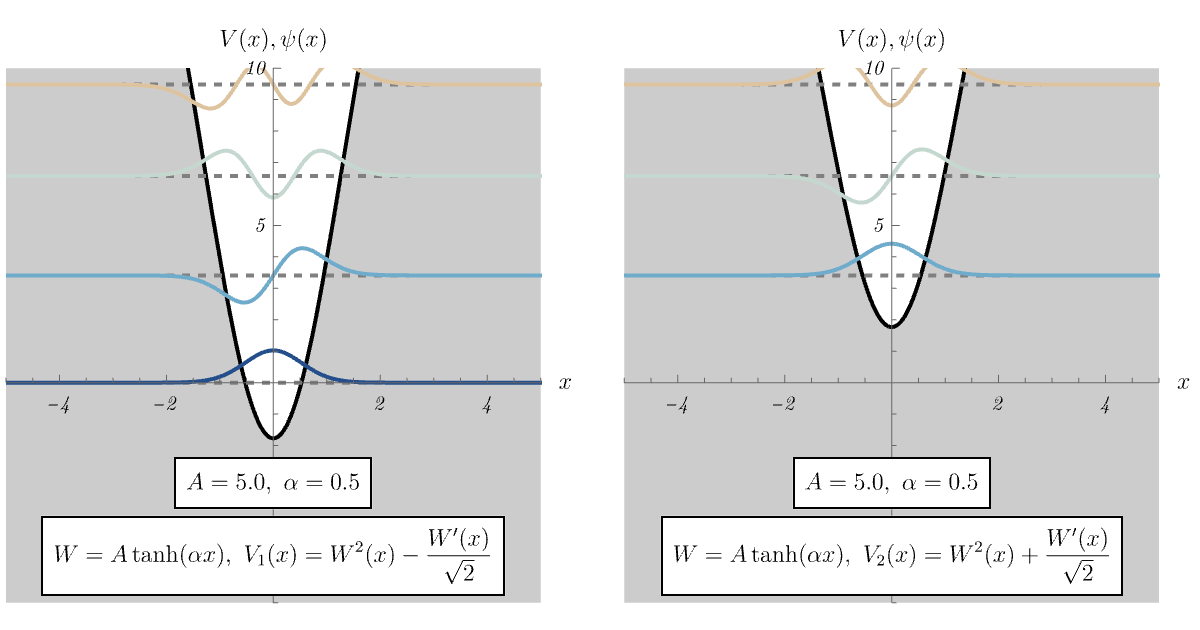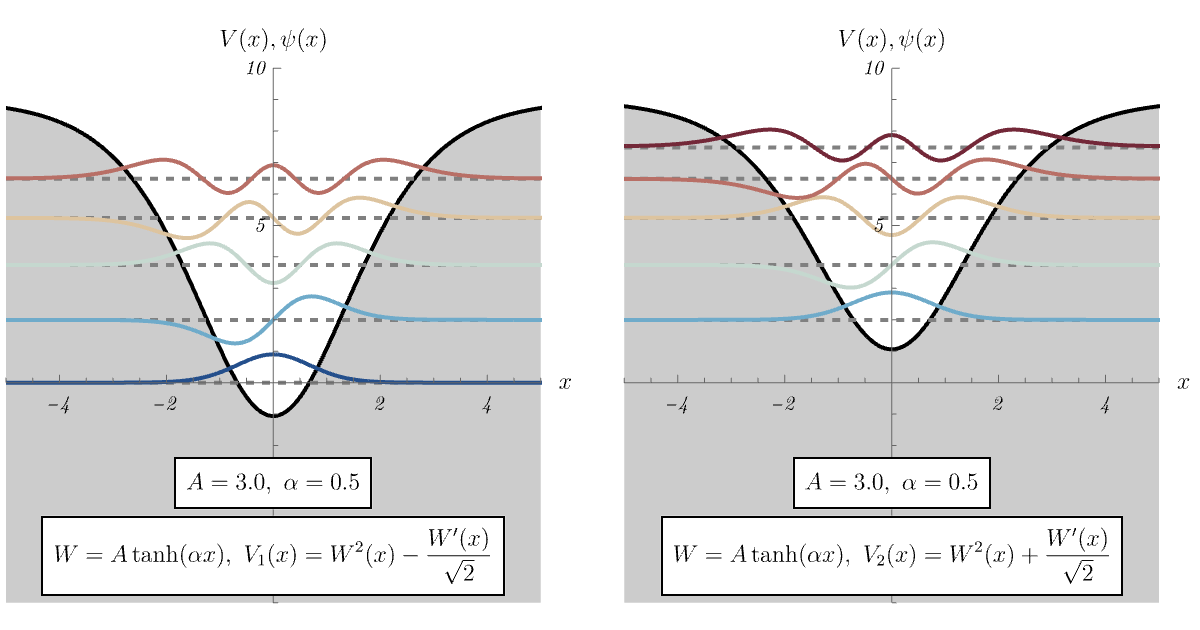
8-3. \( \tanh \)
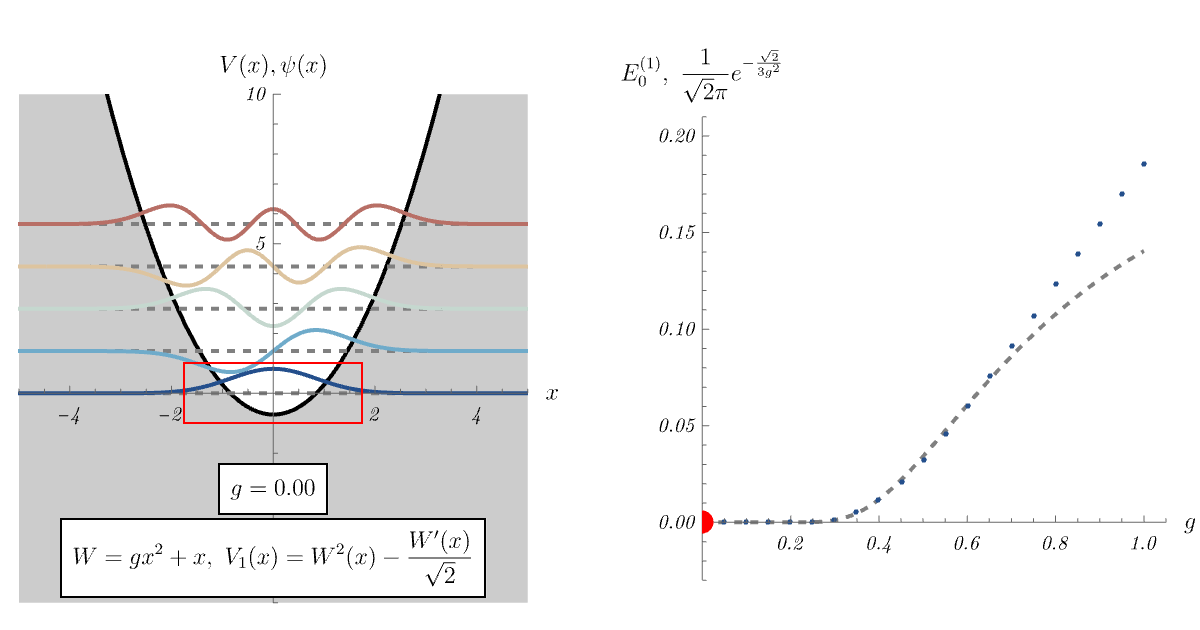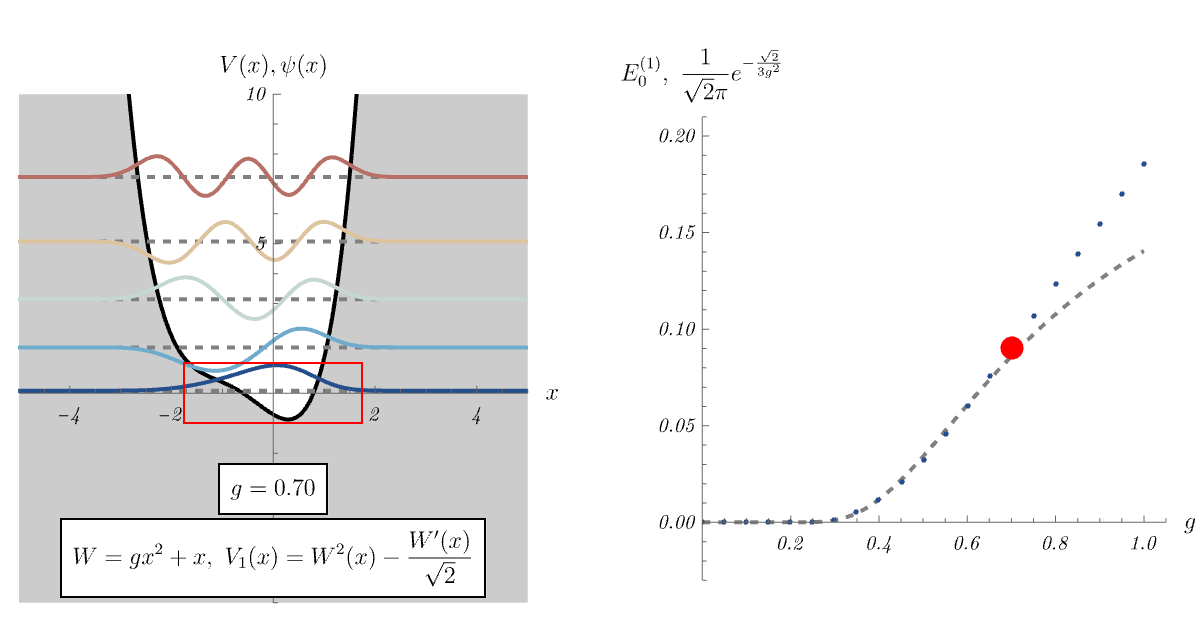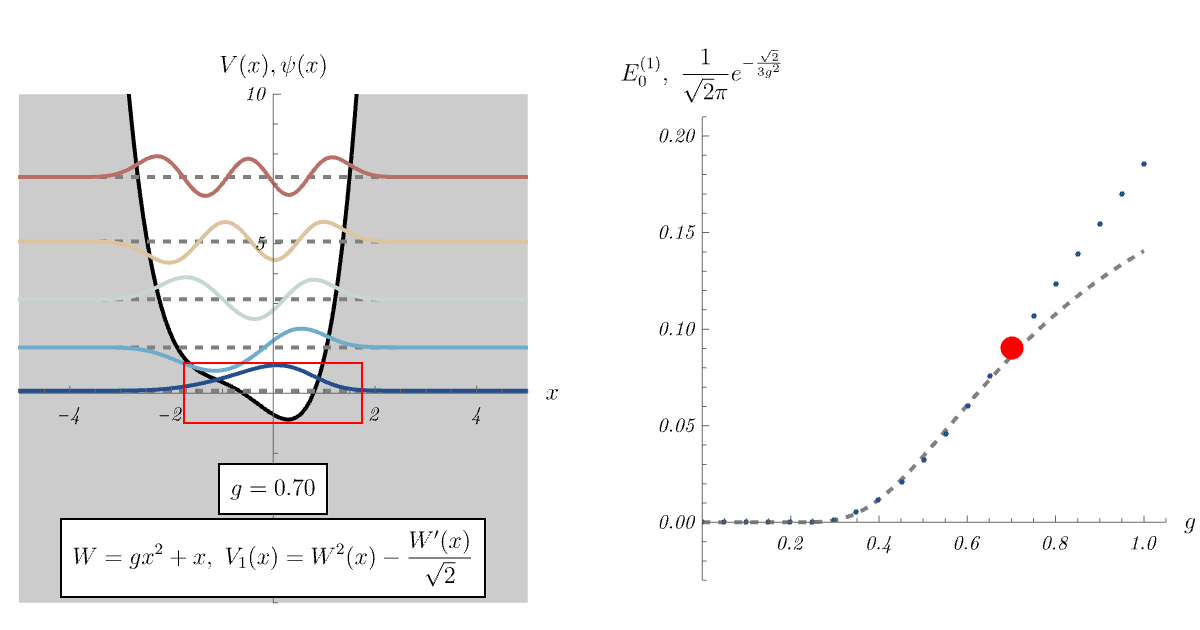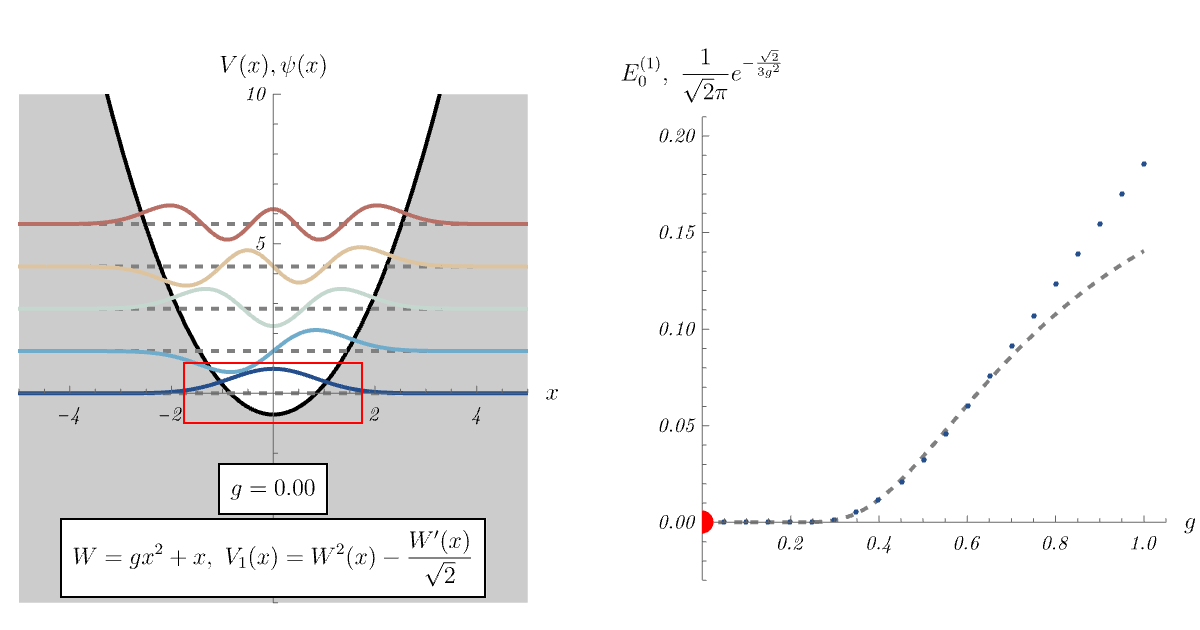
8-4. dynamical SUSY breaking
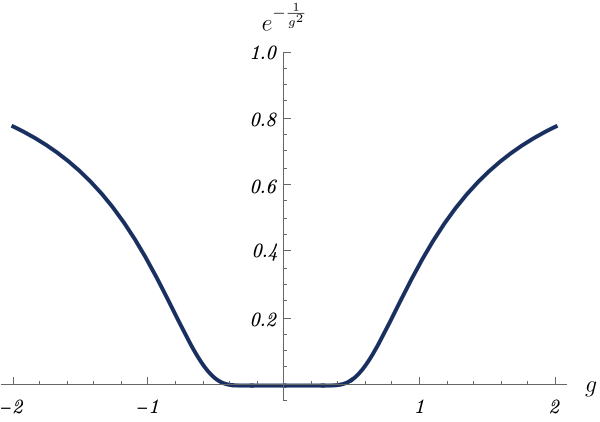
では、\( \hat{A} \ket{\psi_0'} = 0 \) を満たす \( \ket{\psi_0'} \) が存在しない場合はどうなるのだろうか。 この場合、\( \hat{H}_1 \) の基底状態 \( \ket{\psi_0} \) は \( \hat{A} \ket{\psi_0} = 0 \) を満たさない。 すると、対応するエネルギー準位がわずかに \( 0 \) より持ち上がる。 以下、例を見てみよう。