Materials
前回まで、ブラケット表記でのSchrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \ket{\Psi (t)} = \hat{H} \ket{\Psi (t)}, \] について学んできた。 1次元中の粒子であれば \[ \hat{H} = \frac{\hat{p}^2}{2 m} + V (\hat{x}), \] である。 今回はこれがいかに役に立つか、演算子法で調和振動子が「簡単に」解かれる様子を見ることで確認する。 調和振動子のポテンシャルは \[ V (\hat{x}) = \frac{1}{2} m \omega^2 \hat{x}^2, \] である。
7-1. 調和振動子の演算子法:概略
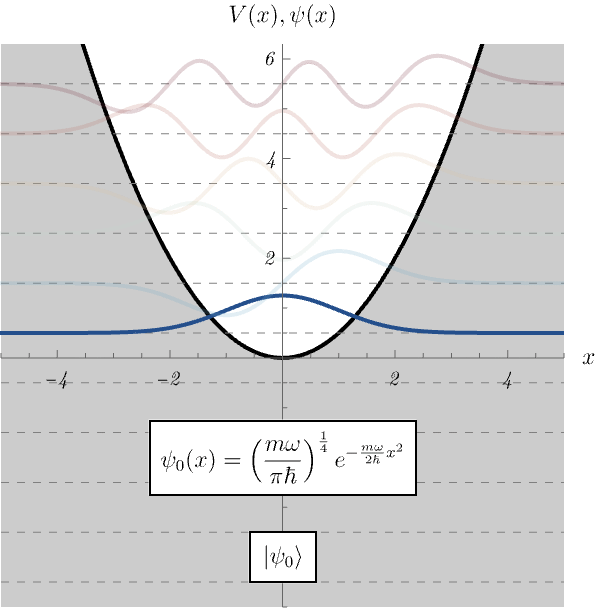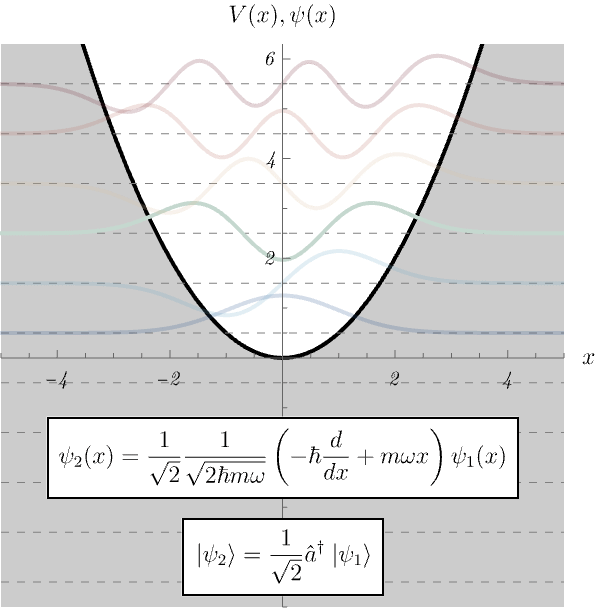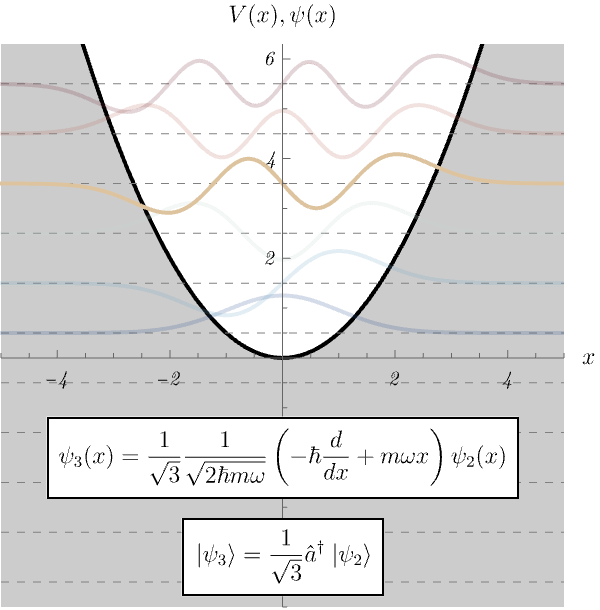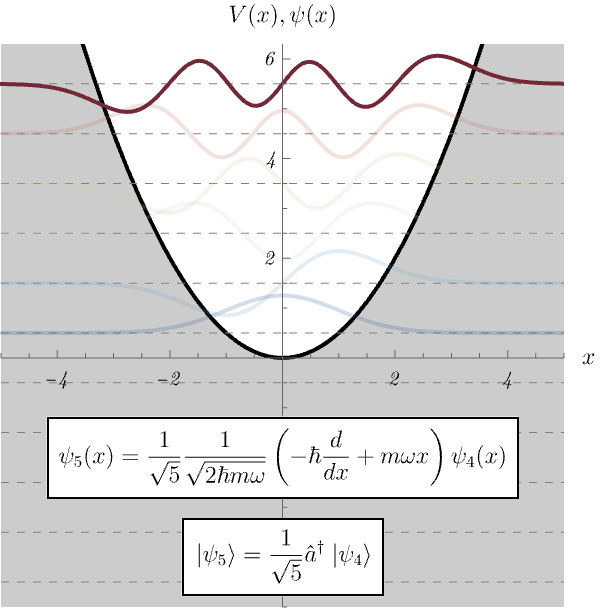
図は以前求めた、調和振動子に対するエネルギー固有状態の波動関数 \( \psi_n (x) \) である。 実は、 \[ \psi_n (x) = \frac{1}{\sqrt{n}} \frac{1}{\sqrt{2 \hbar m \omega}} \left( - \hbar \frac{d}{d x} + m \omega x \right) \psi_{n - 1} (x), \] が成り立っていたことに気付いただろうか。 つまり、\( \psi_n (x) \) は \( \psi_{n - 1} (x) \) を微分したり \( x \) を掛けたりしたものを組み合わせれば作れたのである! こんな式を思い付くのは不可能と思うかもしれない。 しかし、実は演算子法を用いるとこの関係式が簡単に手に入るのである。
\( \hat{x} \) と \( \hat{p} \) をうまく組み合わせた消滅演算子 \( \hat{a} \) および生成演算子 \( \hat{a}^\dagger \) を \[ \hat{a} := \frac{1}{\sqrt{2 \hbar m \omega}} \left( i \hat{p} + m \omega \hat{x} \right), \qquad \hat{a}^\dagger := \frac{1}{\sqrt{2 \hbar m \omega}} \left( - i \hat{p} + m \omega \hat{x} \right), \] としよう。 詳細は以下に述べるが、基底状態 (最低エネルギー状態) \( \ket{\psi_0} \) は \[ \hat{a} \ket{\psi_0} = 0, \] からすぐに求まる。 さらに \( n \) 番目と \( n - 1 \) 番目のエネルギー固有状態 \( \ket{\psi_n},~\ket{\psi_{n - 1}} \) が \[ \ket{\psi_n} = \frac{1}{\sqrt{n}} \hat{a}^\dagger \ket{\psi_{n - 1}}, \] で関係付いていることもすぐにわかる。 この関係式を \( \ket{x} \) 表示で見ると、なんと \[ \braket{x | \psi_n} = \frac{1}{\sqrt{n}} \frac{1}{\sqrt{2 \hbar m \omega}}\bra{x} \hat{a}^\dagger \ket{\psi_{n - 1}} = \frac{1}{\sqrt{n}} \frac{1}{\sqrt{2 \hbar m \omega}} \left( - \hbar \frac{d}{d x} + m \omega x \right) \braket{x | \psi_{n - 1}}, \] に化けるのである。
7-2. 調和振動子の演算子法:詳細
調和振動子に対するHamiltonianは
\[ \qquad \hat{H} = \frac{\hat{p}^2}{2 m} + \frac{1}{2} m \omega^2 \hat{x}^2, \]
であるが、消滅演算子 \( \hat{a} \) および生成演算子 \( \hat{a}^\dagger \) を用いると
\[ \hat{H} = \hbar \omega \left( \hat{a}^\dagger \hat{a} + \frac{1}{2} \right), \]
という簡単な表式になる。
この \( \hat{a} \) と \( \hat{a}^\dagger \) は、\( \hat{H} \) の固有値を \( \hbar \omega \) だけ減らしたり増やしたりする演算子である。
つまり、\( \hat{H} \) の固有値 \( E \) の状態 \( \ket{\psi} \) を持ってくれば、
\[ \begin{array}{ccc}
\vdots && \vdots \\
\hat{H} (\hat{a}^\dagger)^2 \ket{\psi} &=& (E + 2 \hbar \omega) (\hat{a}^\dagger)^2 \ket{\psi}, \\
\hat{H} (\hat{a}^\dagger) \ket{\psi} &=& (E + \hbar \omega) (\hat{a}^\dagger) \ket{\psi}, \\
\hat{H} \ket{\psi} &=& E \ket{\psi}, \\
\hat{H} (\hat{a}) \ket{\psi} &=& (E - \hbar \omega) (\hat{a}) \ket{\psi}, \\
\hat{H} (\hat{a})^2 \ket{\psi} &=& (E - 2 \hbar \omega) (\hat{a})^2 \ket{\psi}, \\
\vdots && \vdots
\end{array}
\]
という、エネルギー \( \left\{ \cdots, E - 2 \hbar \omega, E - \hbar \omega, E, E + \hbar \omega, E + 2 \hbar \omega, \cdots \right\} \) の状態の無限のタワー \( \left\{ \cdots, (\hat{a})^2 \ket{\psi}, (\hat{a}) \ket{\psi}, \ket{\psi}, (\hat{a}^\dagger) \ket{\psi}, (\hat{a}^\dagger)^2 \ket{\psi}, \cdots \right\} \) が作れることになる。
今回、許されるタワーは
\[ \begin{array}{cccc}
\vdots && \vdots \\
\hat{H} (\hat{a}^\dagger)^2 \ket{0} &=& \left( \frac{1}{2} + 2 \right) \hbar \omega (\hat{a}^\dagger)^2 \ket{0}, \\
\hat{H} (\hat{a}^\dagger) \ket{0} &=& \left( \frac{1}{2} + 1 \right) \hbar \omega (\hat{a}^\dagger) \ket{0}, \\
\hat{H} \ket{0} &=& \frac{1}{2} \hbar \omega \ket{0}, \\
\hat{H} (\hat{a}) \ket{0} &=& \left( \frac{1}{2} - 1 \right) \hbar \omega (\hat{a}) \ket{0}, & ただし (\hat{a}) \ket{0} = 0, \\
\hat{H} (\hat{a})^2 \ket{0} &=& \left( \frac{1}{2} - 2 \right) \hbar \omega (\hat{a})^2 \ket{0}, & ただし (\hat{a})^2 \ket{0} = 0, \\
\vdots && \vdots
\end{array}
\]
というエネルギー \( \left\{ \frac{1}{2} \hbar \omega, \frac{3}{2} \hbar \omega, \frac{5}{2} \hbar \omega, \cdots \right\} \) のタワーであり、あるエネルギー以下では \( (\hat{a})^{自然数} \ket{0} = 0 \) のせいで規格化可能な状態が存在しなくなることを見る。
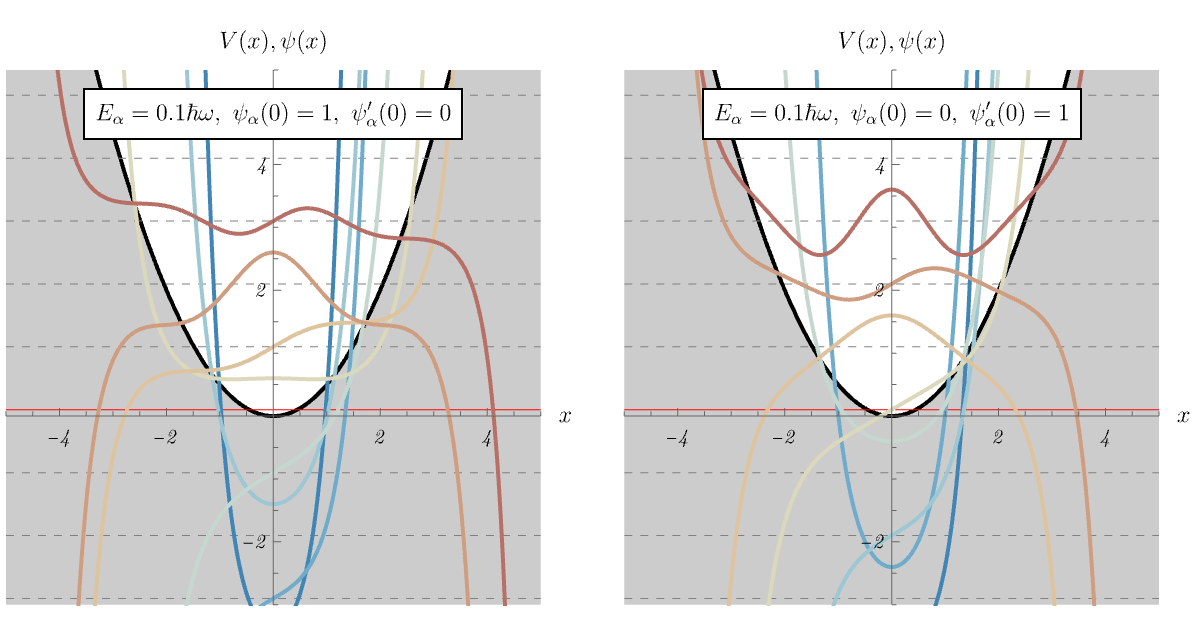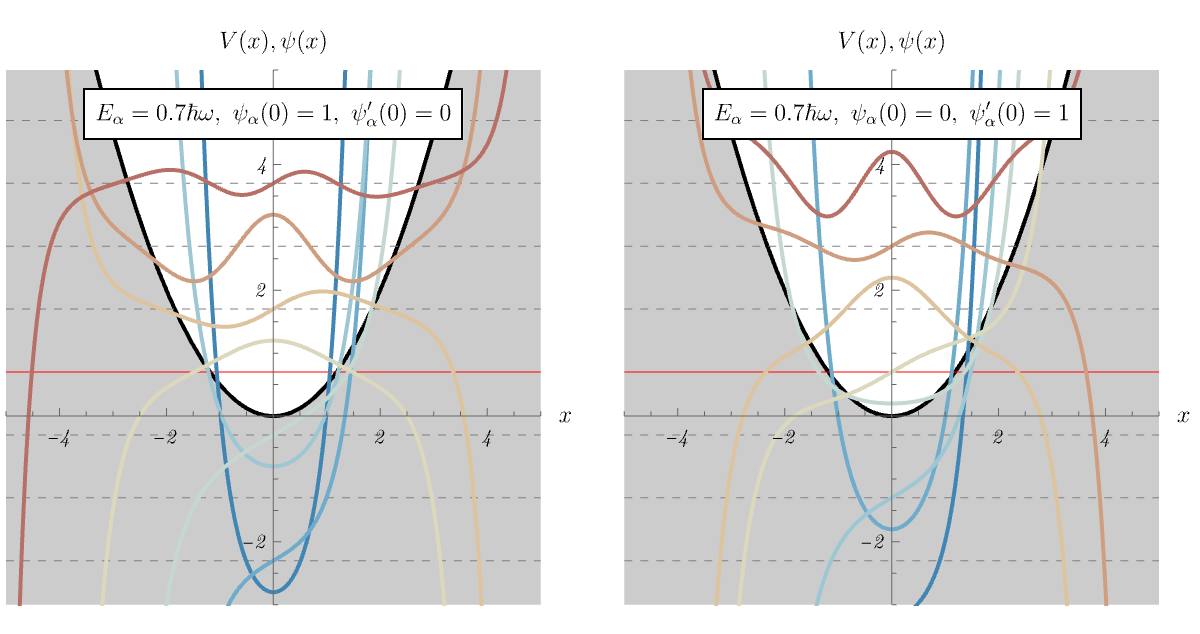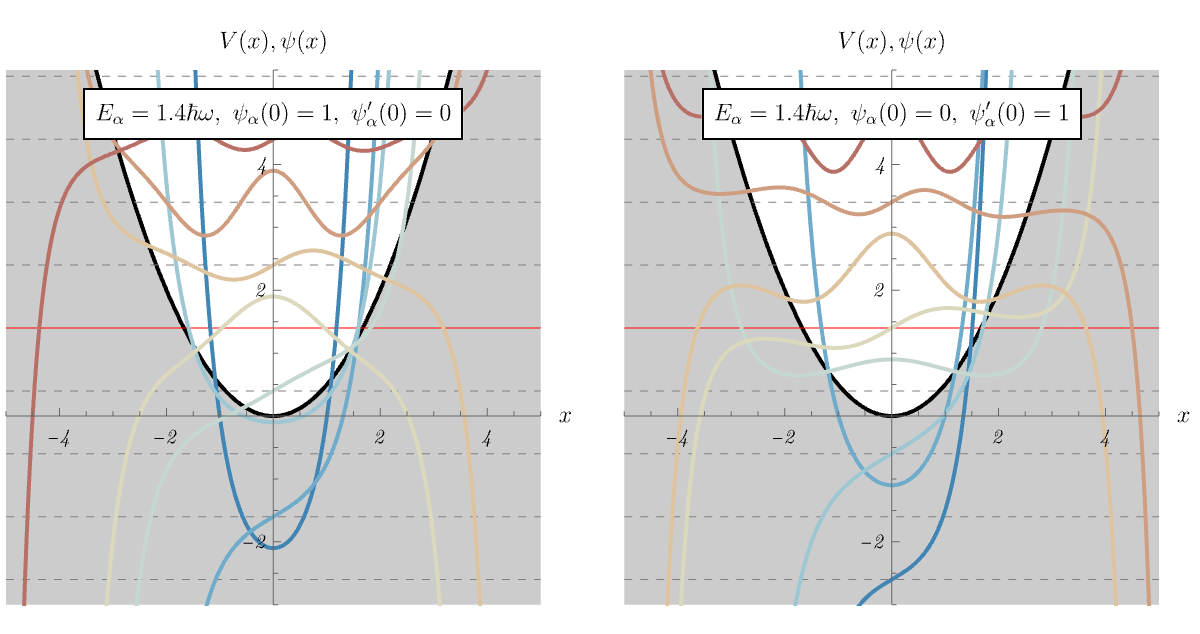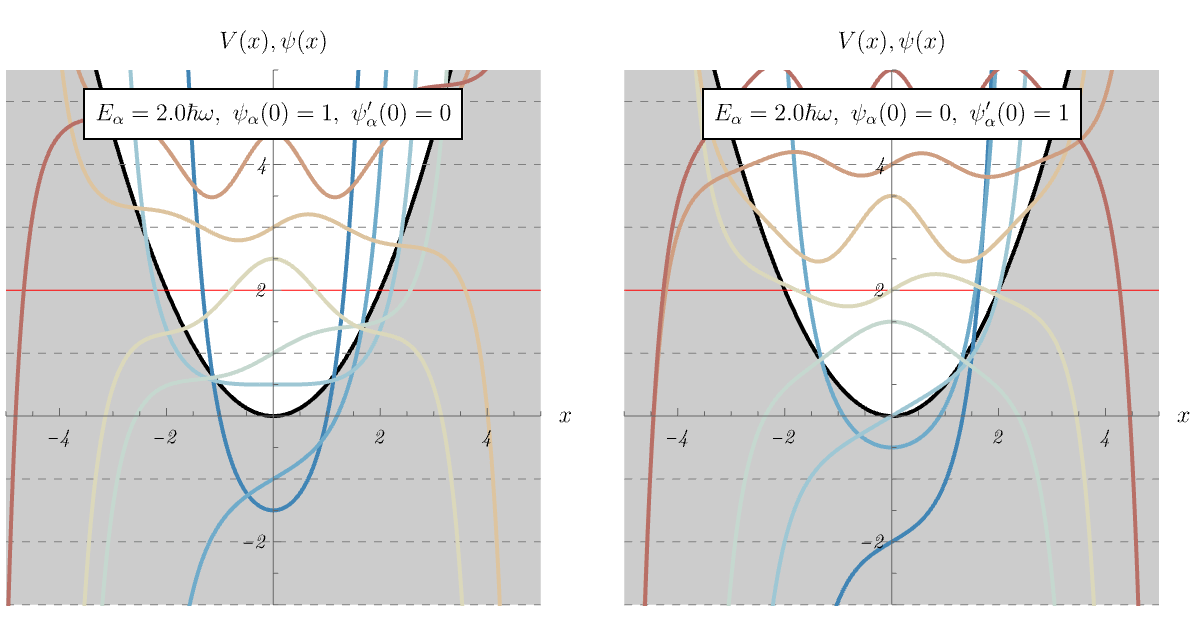
タワーのあるエネルギー以下で状態が \( 0 \) ベクトルになる様子を、視覚的に理解しやすい \( \ket{x} \) 表示で見てみよう。 \( \ket{\psi} \) に \( \hat{a} \) や \( \hat{a}^\dagger \) を当てた状態というのは、\( \ket{x} \) 表示では \[ \bra{x} \hat{a} \ket{\psi} = \bra{x} \frac{1}{\sqrt{2 \hbar m \omega}} \left( i \hat{p} + m \omega \hat{x} \right) \ket{\psi} = \frac{1}{\sqrt{2 \hbar m \omega}} \left( - \frac{d}{d x} + m \omega x \right) \braket{x | \psi}, \] \[ \bra{x} \hat{a}^\dagger \ket{\psi} = \bra{x} \frac{1}{\sqrt{2 \hbar m \omega}} \left( - i \hat{p} + m \omega \hat{x} \right) \ket{\psi} = \frac{1}{\sqrt{2 \hbar m \omega}} \left( \frac{d}{d x} + m \omega x \right) \braket{x | \psi}, \] なので、波動関数 \( \braket{x | \psi} \) がわかっていれば、\( x \) を掛けたり \( x \) で微分したりすることでタワーの一個下や一個上の波動関数が順々に求まる。 \( \hat{a} \) を掛け続けるといくらでもエネルギーが下がってしまうのではないか?と思うかもしれないが、実はそのようなことは起きない。 これを見るため、下図では \( E \) を変えたときに、状態 \( (\hat{a})^n \ket{\psi} \) と \( (\hat{a}^\dagger)^n \ket{\psi} \) に対する \( \ket{x} \) 表示の波動関数 \( \bra{x} (\hat{a})^n \ket{\psi} \) と \( \bra{x} (\hat{a}^\dagger)^n \ket{\psi} \) がどう振る舞うかを示してある。 まず \( \psi (x) = \braket{x | \psi} を \) \[ \left( - \frac{\hbar^2}{2 m} \frac{d^2}{dx^2} + \frac{1}{2} m \omega^2 x^2 \right) \psi (x) = E \psi (x), \] によって解いた後、上記の操作で \( \bra{x} (\hat{a})^n \ket{\psi} \) や \( \bra{x} (\hat{a}^\dagger)^n \ket{\psi} \) を求めている。 \( \psi (x) = \braket{x | \psi} \) を求める時の境界条件は \( \psi (x) = 1 \) (左図) もしくは \( \psi' (x) = 1 \) (右図)に設定してある。 発散しない \( \psi (x) \) が得られるのは \[ E = \left( n + \frac{1}{2} \right) \hbar \omega, \] の時だけであるが、その場合には負のエネルギー準位の波動関数が全て \( 0 \) になることがわかる。