Materials
今回は不確定性関係 \[ \sigma_A^2 \sigma_B^2 \geq \left( \frac{1}{2 i} \braket{[\hat{A}, \hat{B}]} \right)^2 \left(= \left( \frac{1}{2 i} \bra{\Psi} [\hat{A}, \hat{B}] \ket{\Psi} \right)^2 \right), \] について学ぶ。 \( \sigma_A,~\sigma_B \) は物理量 \( \hat{A},~\hat{B} \) を観測した際の分散 \[ \sigma_A^2 := \braket{(\hat{A} - \braket{\hat{A}})^2} \left(= \bra{\Psi} (\hat{A} - \bra{\Psi} \hat{A} \ket{\Psi})^2 \ket{\Psi}\right), \] \[ \sigma_B^2 := \braket{(\hat{B} - \braket{\hat{B}})^2} \left(= \bra{\Psi} (\hat{B} - \bra{\Psi} \hat{B} \ket{\Psi})^2 \ket{\Psi}\right), \] である。 不確定性関係は、物理量 \( \hat{A},~\hat{B} \) をある精度以上で定めることが不可能であることを教えてくれる。
まずはアニメーションを見てみよう。 これは調和振動子ポテンシャル下での(位置表示の)Schrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \Psi (t, x) = H \Psi (t, x), \qquad H = - \frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2} + V (x), \] を適当な初期条件で解いた結果である。 上段図の青線・黄線・緑線はそれぞれ \( {\rm Re} \Psi (t, x),~{\rm Im} \Psi (t, x),~|\Psi (t, x)|^2\) である。 数値計算では \( m = \omega = \hbar = 1 \) と置いてある。 粒子がポテンシャルの端点付近にいるときは位置に関してピークを持ち、逆にポテンシャルの底付近にいるときは平面波に近い分布を持つ(= 運動量に関してピークを持つ)ことがわかる。
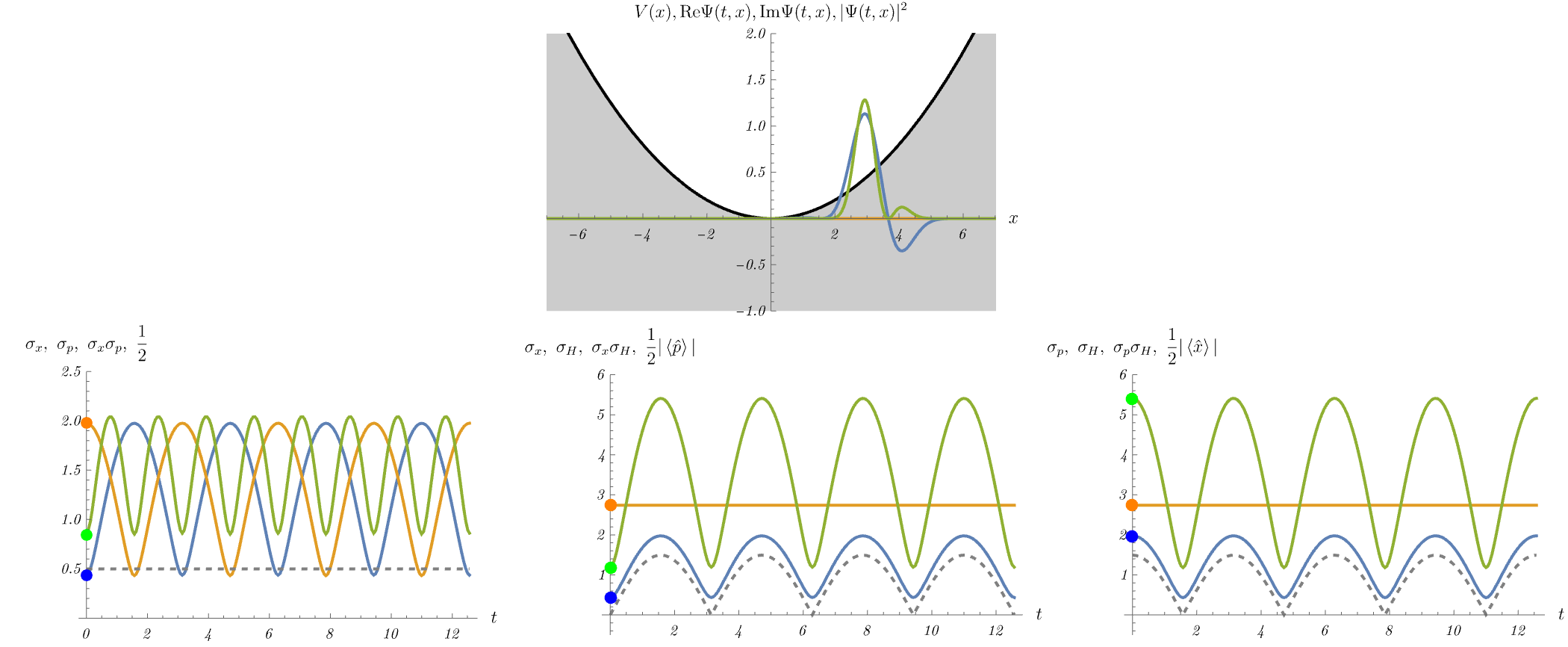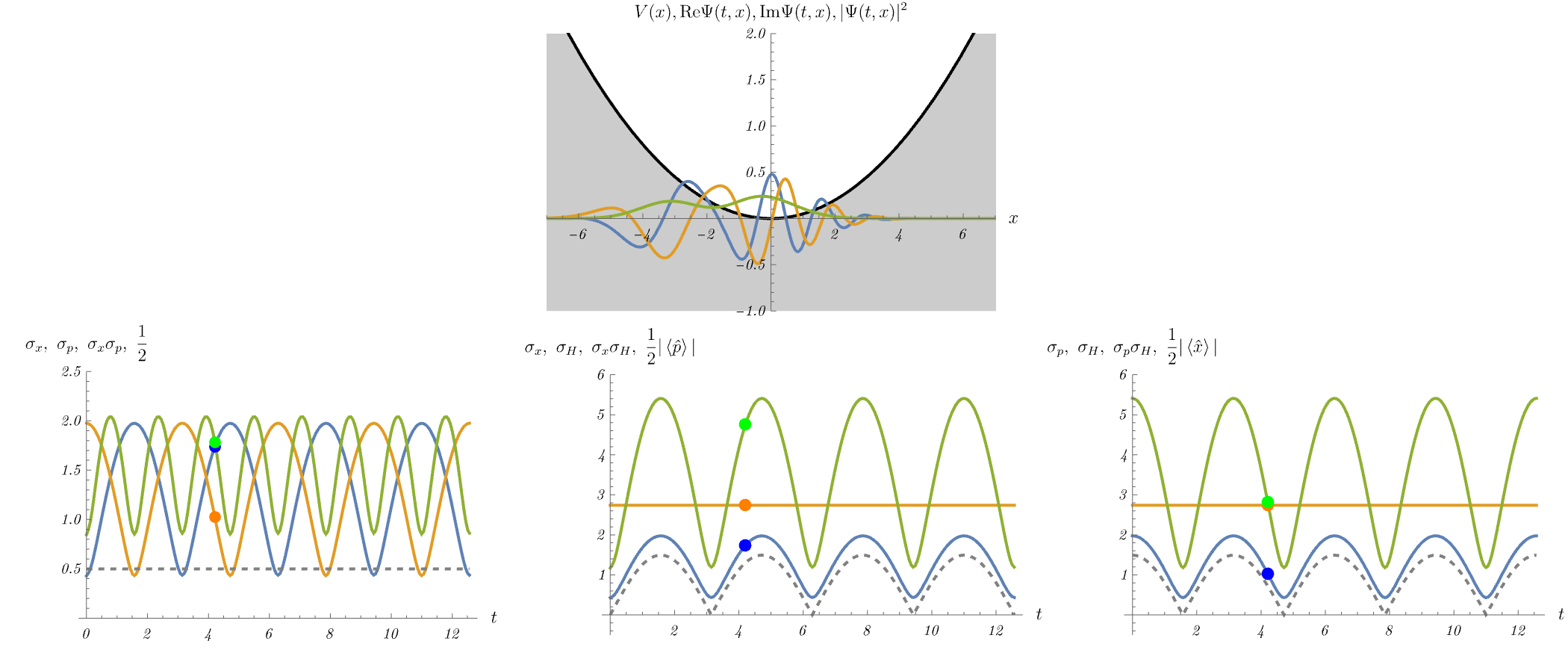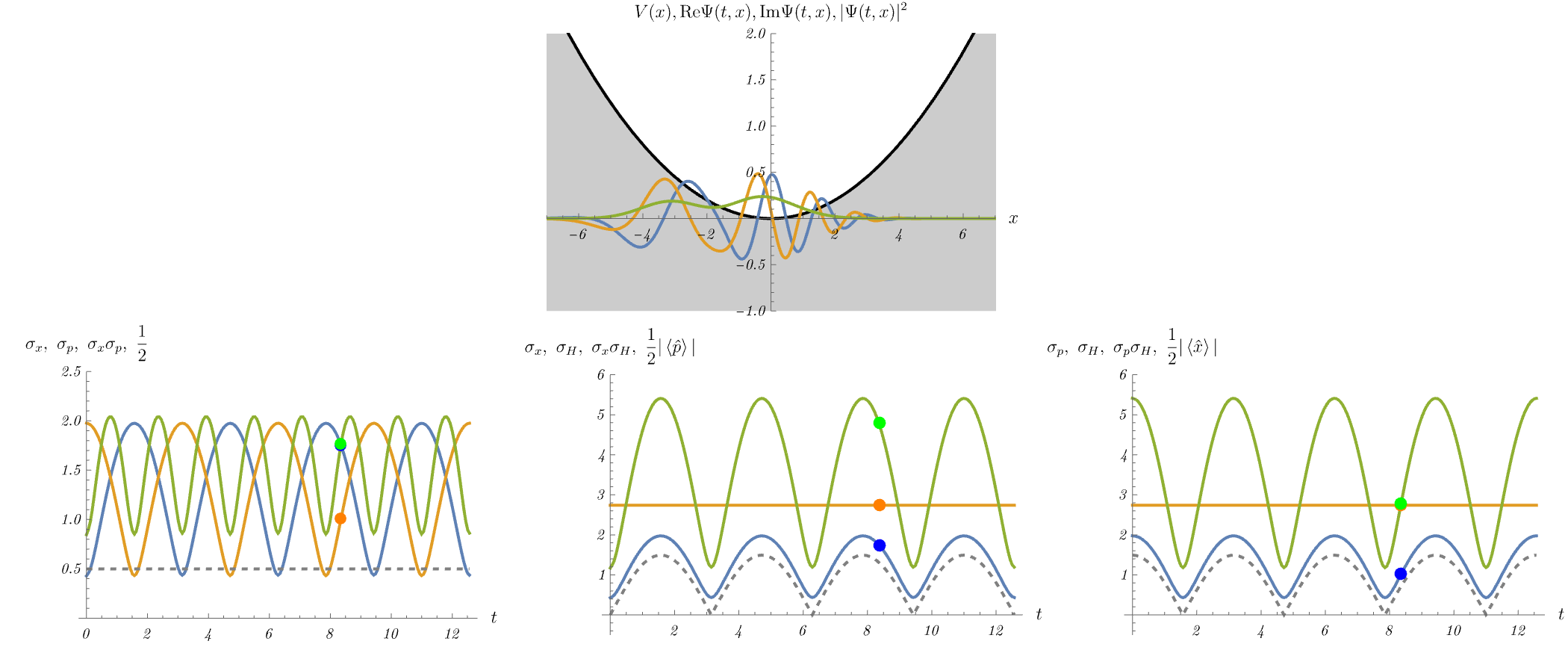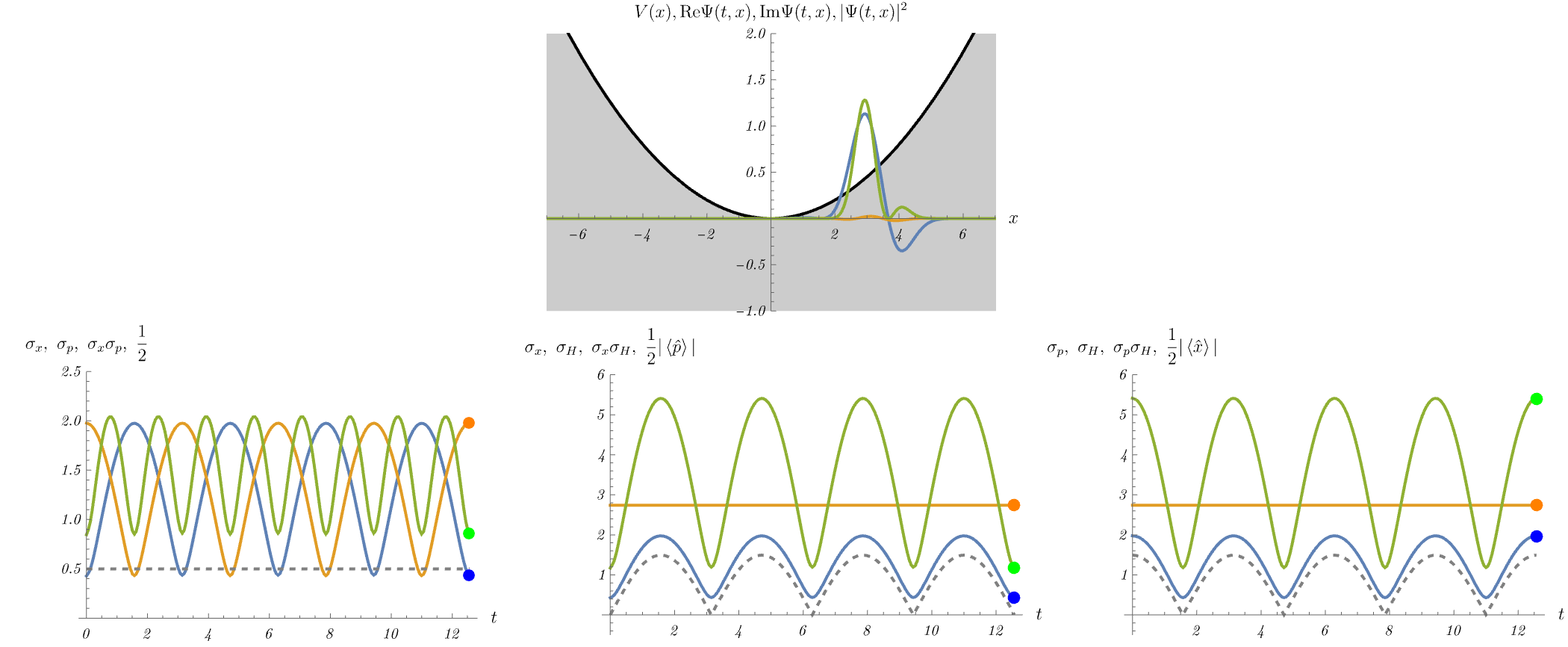
6-1. 位置と運動量の不確定性関係
不確定性関係のうち最もよく知られたものは、位置と運動量の不確定性関係 \[ \sigma_x^2 \sigma_p^2 \geq \left( \frac{1}{2 i} \bra{\Psi} [\hat{x}, \hat{p}] \ket{\Psi} \right)^2 = \left( \frac{1}{2} \hbar \right)^2, \] である。 \( \hat{x} \) と \( \hat{p} \) の交換関係は定数であるため、不確定性関係の右辺も定数になる。 下段左図の青線・黄線・緑線はそれぞれ位置の分散の平方根 \( \sigma_x \)、運動量の分散の平方根 \( \sigma_p \)、およびそれらの積 \( \sigma_x \sigma_p \) である。 不確定性関係によると \( \sigma_x \sigma_p \) (緑線)は \( \frac{1}{2} \hbar \) (点線) 以上であるが、これが確かに成り立っていることがわかる。 ところで、粒子がポテンシャルの端点付近あるいは底付近にいるときの \( \sigma_x,~\sigma_p \) を見てみると、端点付近では \( \sigma_x \) が小さく、底付近では \( \sigma_p \) が小さいことがわかる。 これは端点付近で粒子は位置に関してピークを持ち、底付近で平面波に近い分布を持つ(= 運動量に関してピークを持つ)ことが理由である。
6-2. 位置とエネルギーの不確定性関係
不確定性関係は位置と運動量だけに成り立つ関係ではない。 例えば、位置とHamiltonianの不確定性関係は、\( \hat{A} = \hat{x},~\hat{B} = \hat{H} \) とすることで \[ \sigma_x^2 \sigma_H^2 \geq \left( \frac{1}{2 i} \bra{\Psi} [\hat{x}, \hat{H}] \ket{\Psi} \right)^2 = \left( \frac{\hbar}{2 m} \bra{\Psi} \hat{p} \ket{\Psi} \right)^2, \] と求められる。 右辺が定数ではないことに注意しよう。 下段中央図の青線・黄線・緑線はそれぞれそれぞれ位置の分散の平方根 \( \sigma_x \)、Hamiltonianの分散の平方根 \( \sigma_H \)、およびそれらの積 \( \sigma_x \sigma_H \) である。 不確定性関係によると \( \sigma_x \sigma_H \) (緑線)は \( \frac{\hbar}{2 m} |\bra{\Psi} \hat{p} \ket{\Psi}| \) (点線) 以上であるが、これが確かに成り立っていることがわかる。
6-3. 運動量とエネルギーの不確定性関係
同様に、運動量とHamiltonianの不確定性関係は、\( \hat{A} = \hat{p},~\hat{B} = \hat{H} \) とすることで \[ \sigma_p^2 \sigma_H^2 \geq \left( \frac{1}{2 i} \bra{\Psi} [\hat{p}, \hat{H}] \ket{\Psi} \right)^2 = \left( - \frac{\hbar m \omega^2}{2} \bra{\Psi} \hat{x} \ket{\Psi} \right)^2, \] と求められる。 右辺が定数ではないことに注意しよう。 下段右図の青線・黄線・緑線はそれぞれそれぞれ運動量の分散の平方根 \( \sigma_p \)、Hamiltonianの分散の平方根 \( \sigma_H \)、およびそれらの積 \( \sigma_p \sigma_H \) である。 不確定性関係によると \( \sigma_p \sigma_H \) (緑線)は \( \frac{\hbar m \omega^2}{2} |\bra{\Psi} \hat{x} \ket{\Psi}| \) (点線) 以上であるが、これが確かに成り立っていることがわかる。