Materials
前回は波動関数をブラケット表示で書く方法について学んだ。 今回は、系の状態 \( \left| \Psi (t) \right> \) の発展を記述するSchrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \left| \Psi (t) \right> = \hat{H} \left| \Psi (t) \right>, \] について学ぶ。
5-1. Schrödinger方程式と波動関数 - 例1
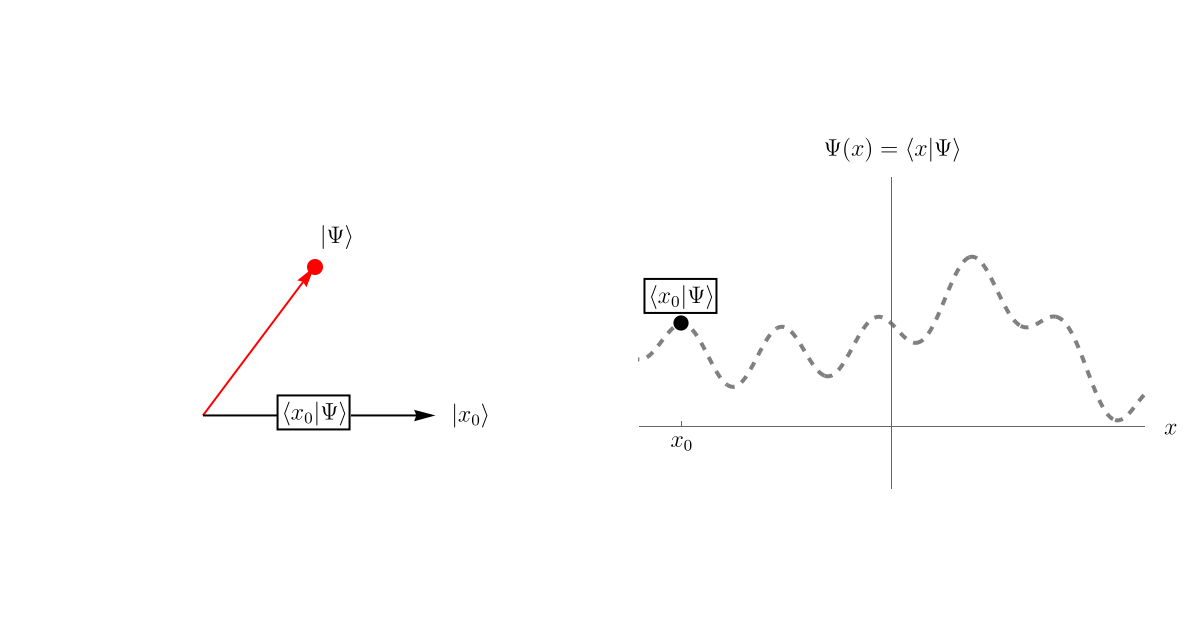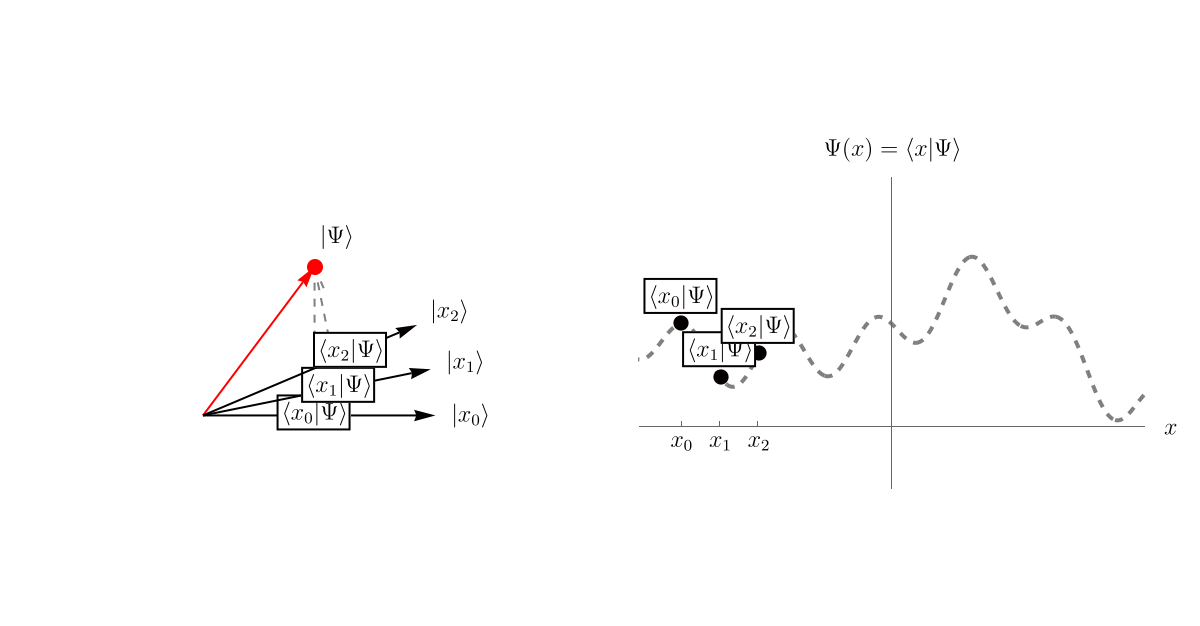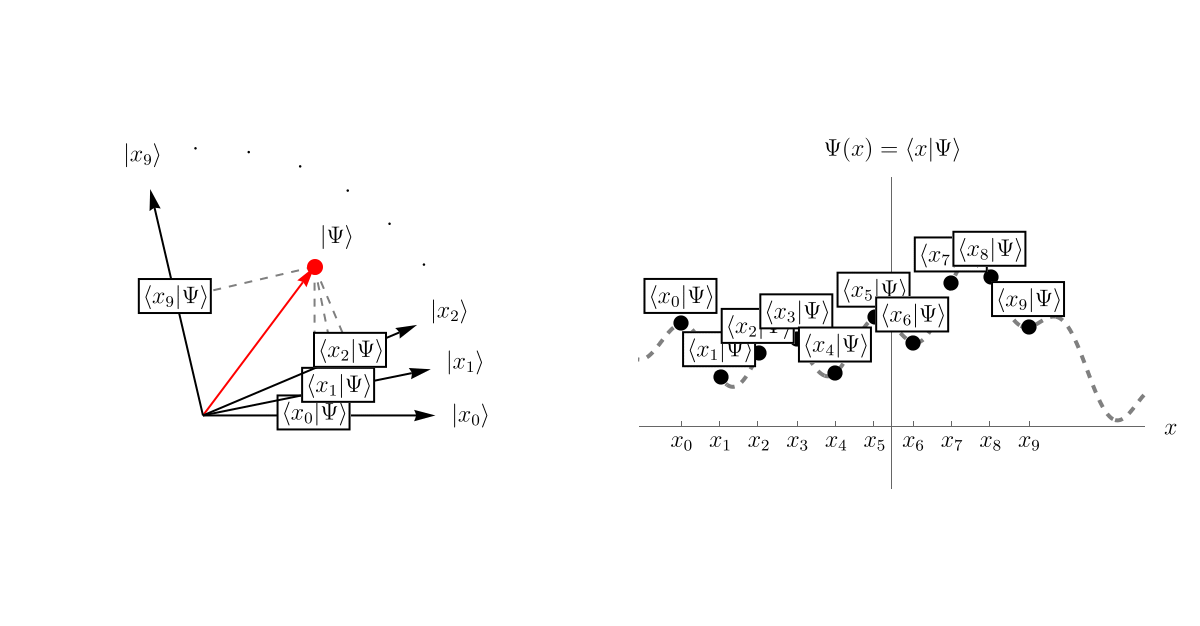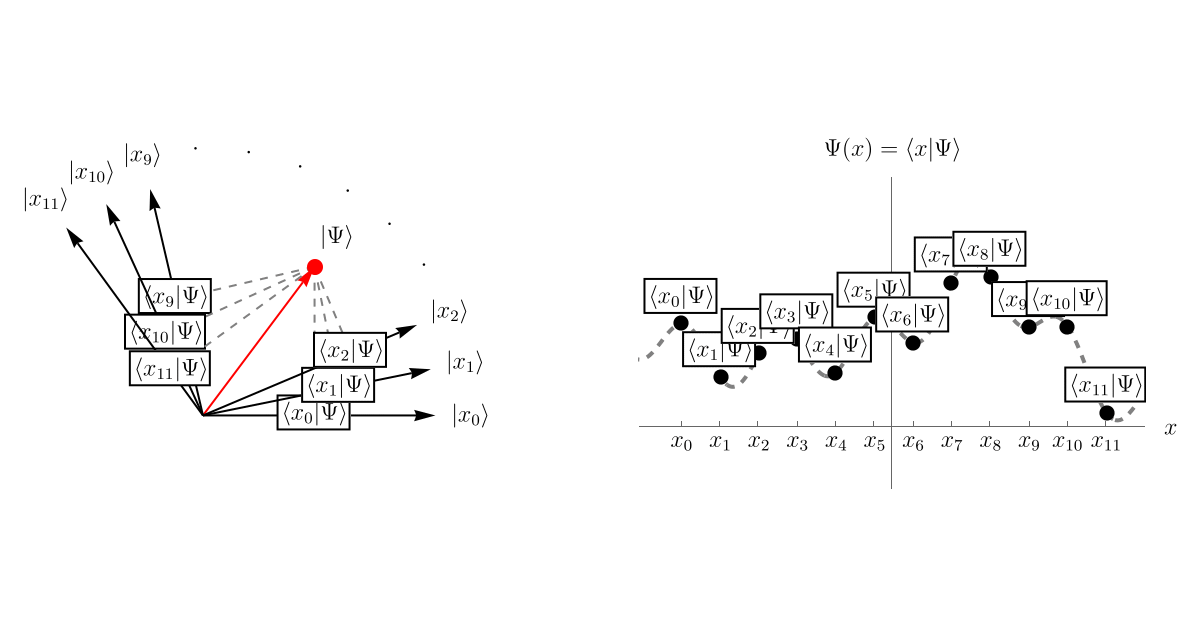
まず、前回の内容をおさらいしよう。 「系の状態」が抽象的なベクトル \( \left| \Psi \right> \) として表されている。 この \( \left| \Psi \right> \) を表示するために、基底として無限個のベクトル \( \left\{ \left| x \right> \right\} \) を用意しよう。 それぞれの \( \left| x \right> \) はHermite演算子 \( \hat{x} \) の固有ベクトルであり、対応する固有値は \( x \) である。 異なる固有値 \( x, x' \) に属するベクトルは直交している。 \[ \left< x | x' \right> = \delta (x - x'). \] そして、波動関数 \( \Psi (t, x) \) というのは、\( \left| \Psi \right> \) を基底 \( \left\{ \left| x \right> \right\} \) で表示したときの係数 \( \left< x | \Psi \right> \)、つまり \( \left| \Psi \right> \) の中に \( \left| x \right> \) がどれだけ存在するかである。 以下のアニメーションは単に概念を説明するためのもので、左図の \( \left< x_i | \Psi \right> \) の値と右図の \( \left< x_i | \Psi \right> \) の値を数値的に一致させてはいないことに注意しよう。
この \( \left| \Psi \right> \) がSchrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \left| \Psi (t) \right> = \hat{H} \left| \Psi (t) \right>, \] に従って時間発展すると、\( \left| x \right> \) との内積が時々刻々変化する。 これが波動関数 \( \Psi (t, x) = \left< x | \Psi (t) \right> \) の時間発展である。 以下のアニメーションは先程と同じく、左図の \( \left< x_i | \Psi \right> \) の値と右図の \( \left< x_i | \Psi \right> \) の値を数値的に一致させてはいないことに注意しよう。
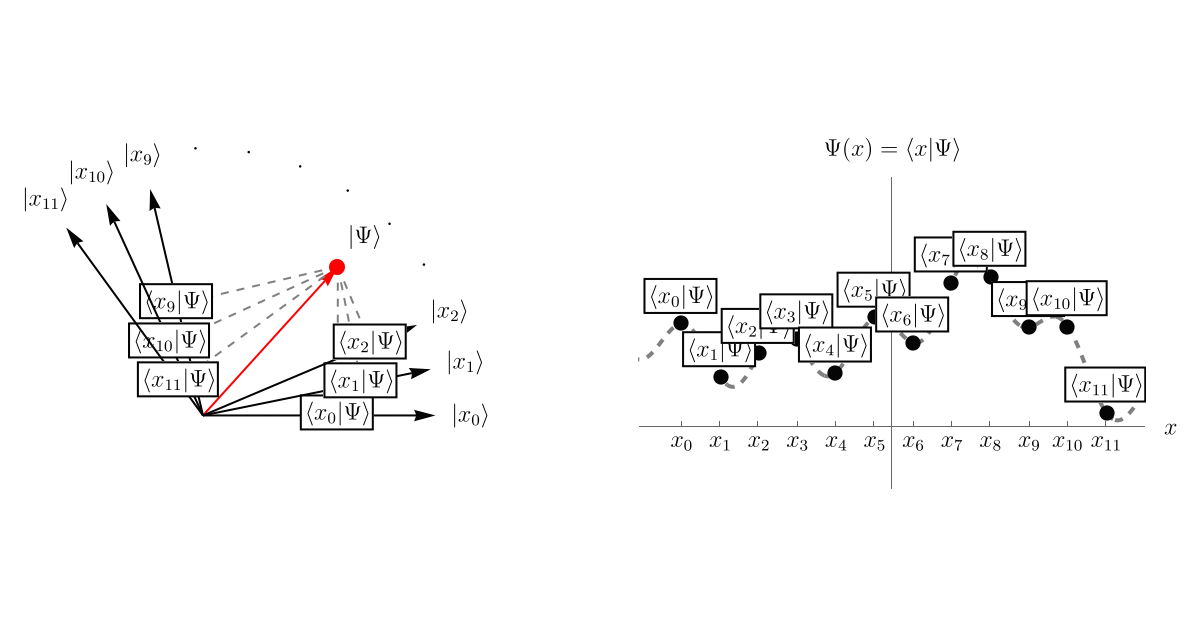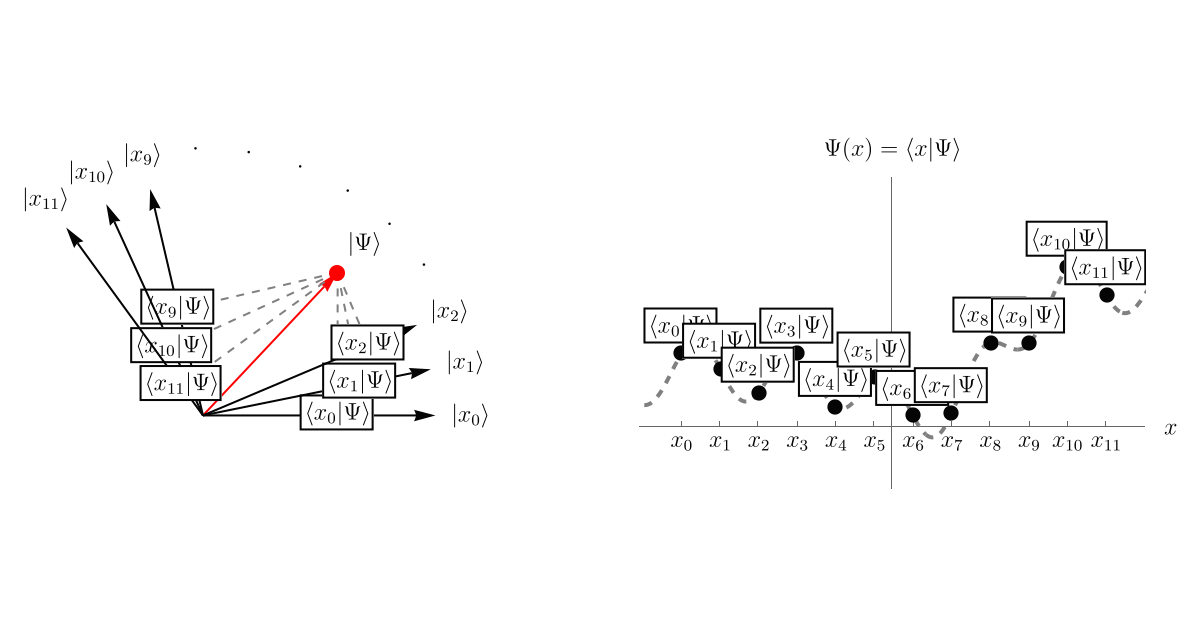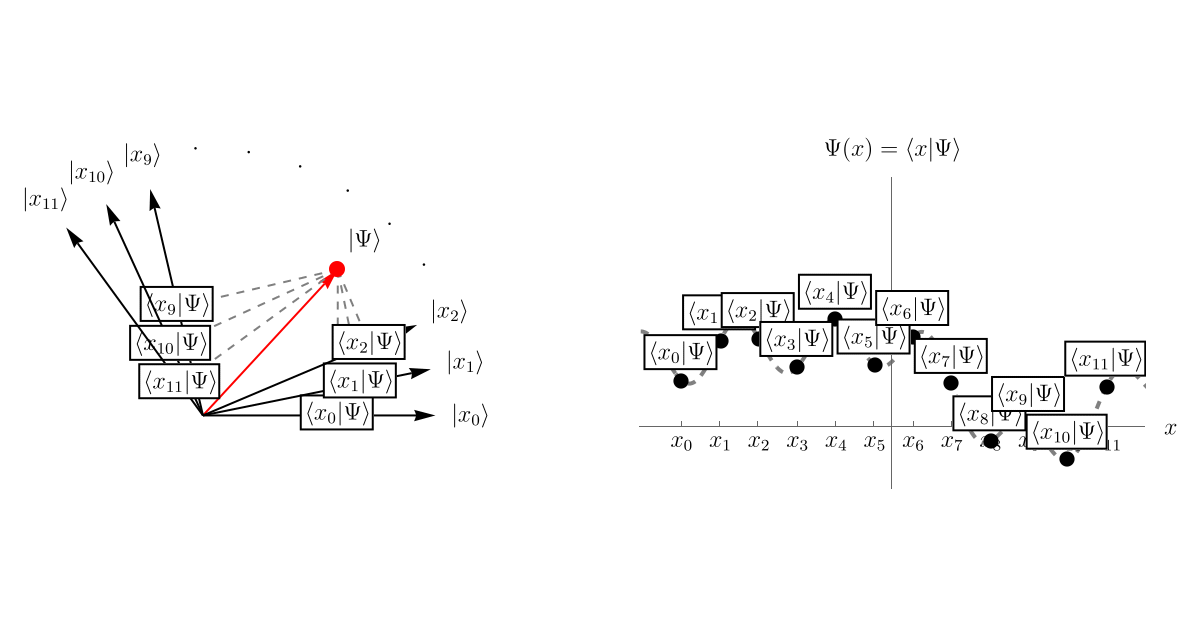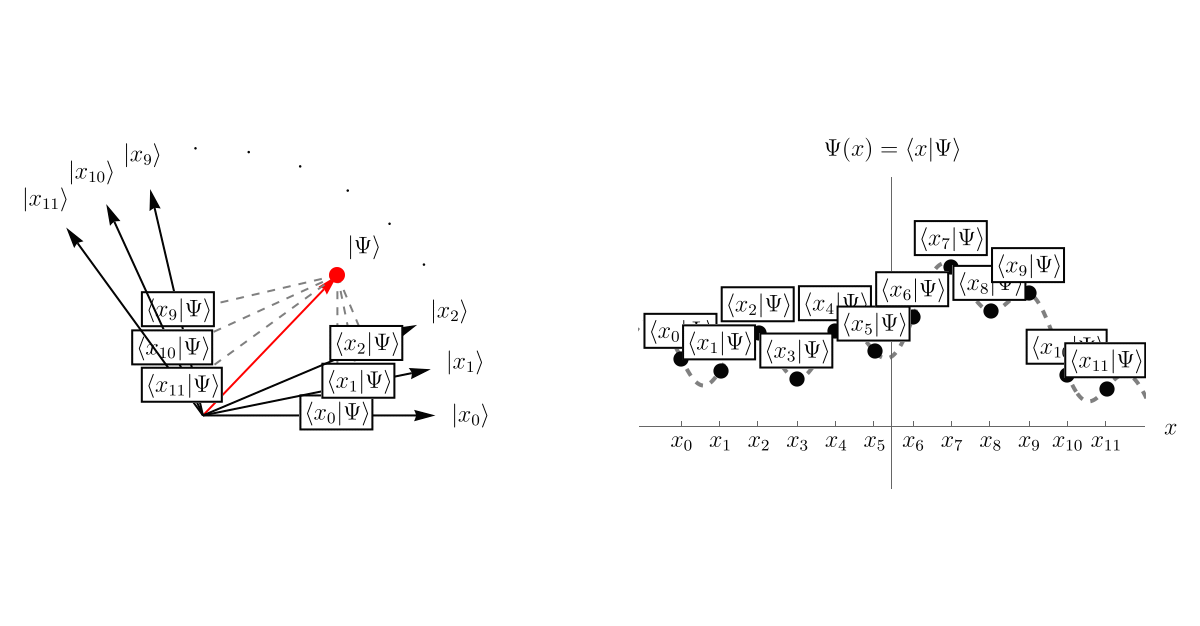
5-2. Schrödinger方程式と波動関数 - 例2
さて、Schrödinger方程式を抽象化させたメリットはどこにあるのだろうか。 Newtonの運動方程式 \( m a = F \) を例に出してみよう。 これが言っているのは、「 力 \( F \) という、作用・反作用の法則 (= 押した分だけ押し返される) などの性質を満たす装置を導入すると、物体の運動がうまく説明できる」ということである。 \( F \) をどう選べばいいのか?という問いに対しては、「\( F \) は考えたい系に応じて異なる形を適切に見つけなければならない」が答えであった。 例えばばねであれば \( F = - k x\)、万有引力であれば \( F = - \frac{G m M}{r^2} \) である。
Schrödinger方程式の話に戻ろう。 これが言っているのは、「Schrödinger方程式を導入すると、量子的な系の時間発展がうまく説明できる」ということである。 Hamiltonian \( \hat{H} \) をどう選べばいいのか?という問いに対しては、Newtonの運動方程式の場合と同じく「\( \hat{H} \) は考えたい系に応じて異なる演算子を適切に見つけなければならない」が答えである。 また、ベクトル \( \left| \Psi \right> \) の次元も系に応じて適切に取らなければならない。 なので、前々回まで扱ってきた \(H \overset{表示}{=} - \frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2} + V (x) \) (= 演算子で書くと \(\hat{H} = \frac{\hat{p}^2}{2 m} + V (\hat{x}) \)) はあくまで1つの例なのである。
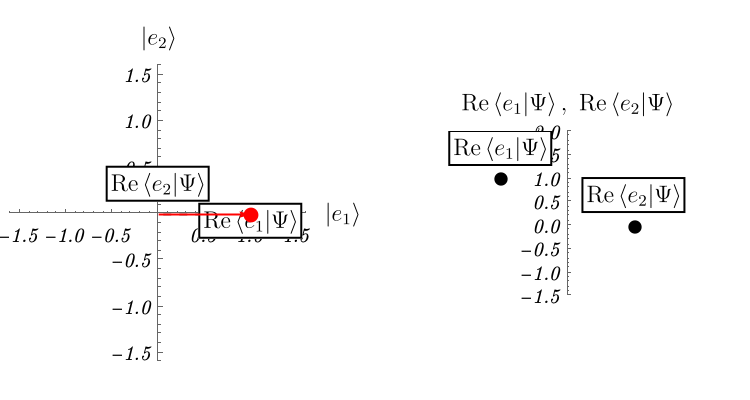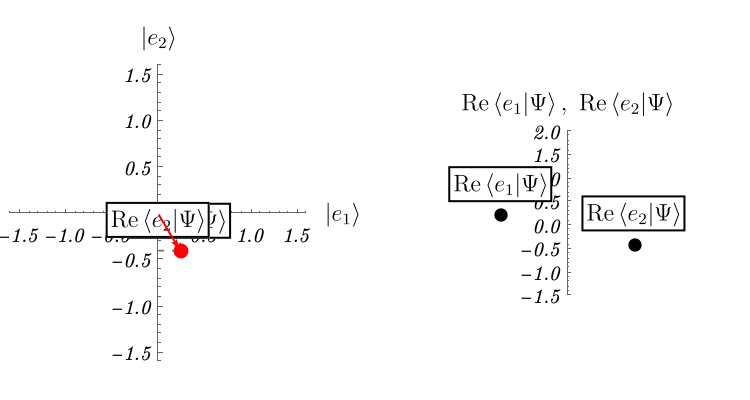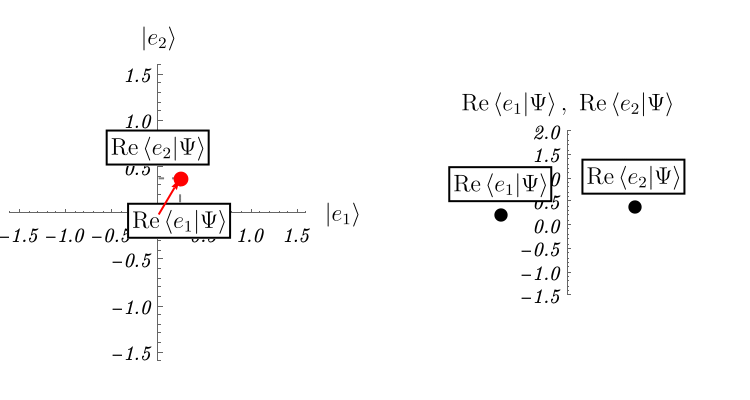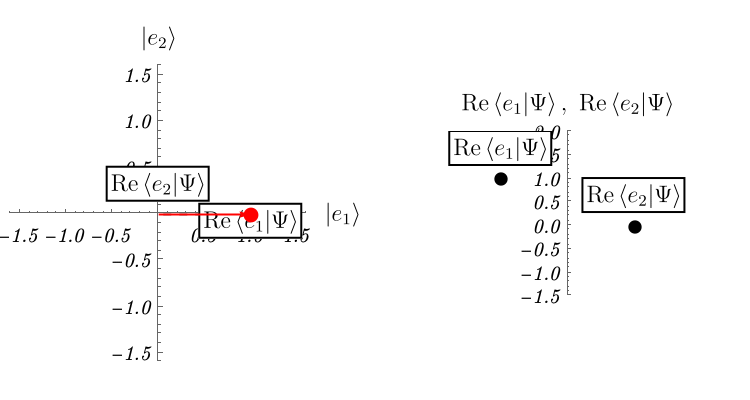
では他にどのような例があるのだろうか。 ここでは2準位系と呼ばれる、2次元のHilbert空間で記述される系の振る舞いを紹介する。 2次元なので、基底は2つあればよい。 それらを \( \left| e_1 \right>, \left| e_2 \right> \) としよう。 成分で表示すると \[ \left| e_1 \right> \overset{表示}{=} \left( \begin{array}{c} 1 \\ 0 \end{array} \right), \qquad \left| e_2 \right> \overset{表示}{=} \left( \begin{array}{c} 0\\ 1 \end{array} \right), \] である。
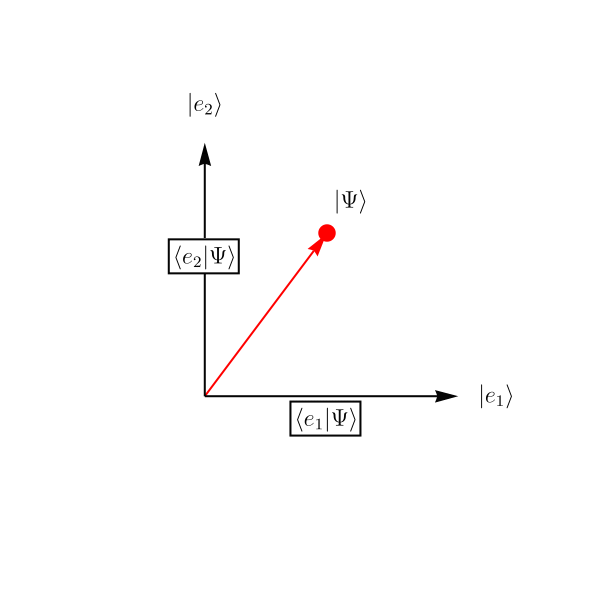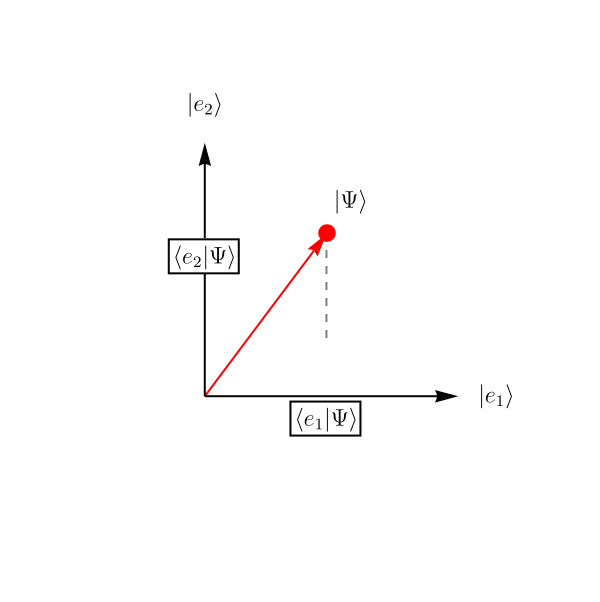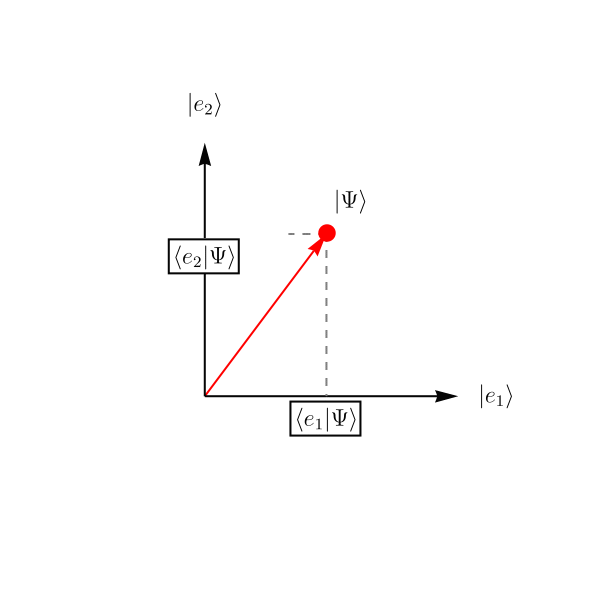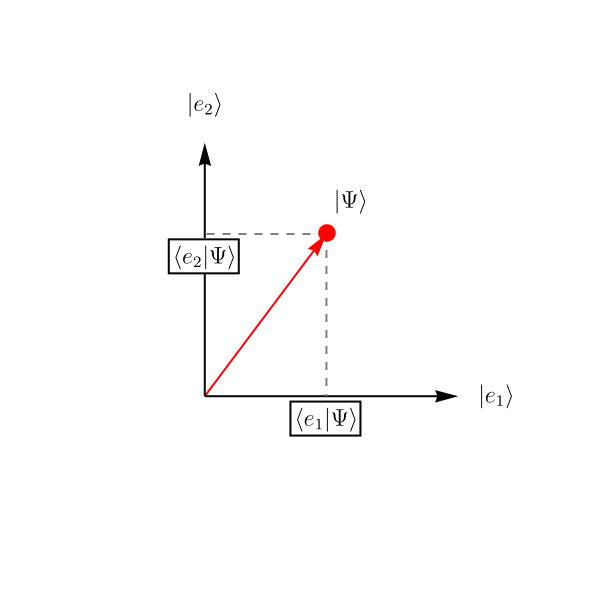
この系がSchrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \left| \Psi (t) \right> = \hat{H} \left| \Psi (t) \right>, \qquad \hat{H} \overset{表示}{=} \left( \begin{array}{cc} 1 & \epsilon \\ \epsilon & 1 \end{array} \right), \] に従って時間発展するとしよう。 理論のパラメータを \( \epsilon = 0.2\)、初期条件を \( \left| \Psi (t = 0) \right> \overset{表示}{=} \left( \begin{array}{c} 1 \\ 0 \end{array} \right) \) として解いたものが下図である。 複素数は表示できないので、実部だけ表示してある。 これは実際にSchrödinger方程式を数値的に解いた結果である。 \( x \) 空間の波動関数とは単にHilbert空間 (= \( \left| \Psi \right> \) の属するベクトル空間) の次元が異なるだけで、概念的には何ら変わらないことがわかるだろうか。