Materials
今回はブラケット記法あるいはDiracの記法と呼ばれるものを学ぶ。 これは、ベクトルを \(\vec{\Psi}\) と書く代わりに \(\left| \Psi \right>\) と書く記法である。
4-1. 基底
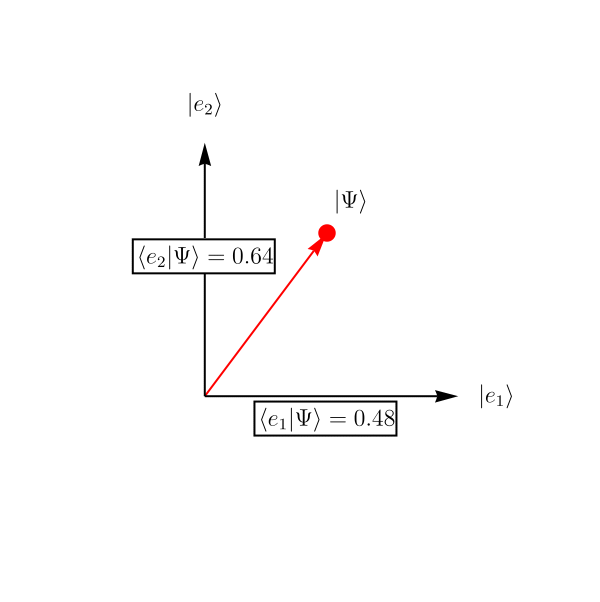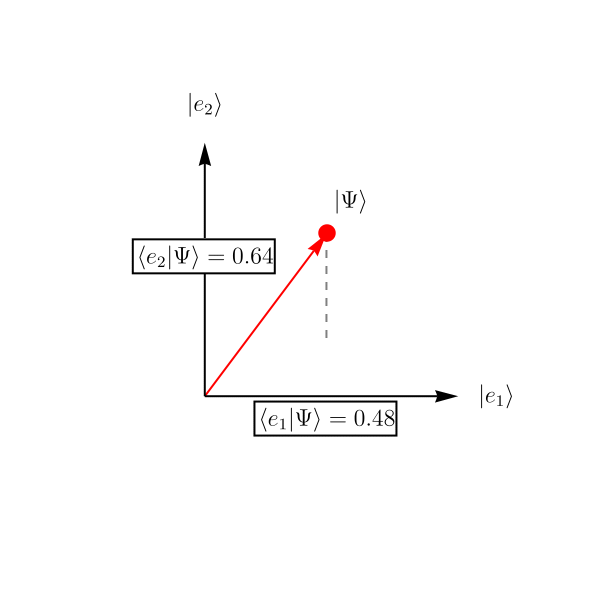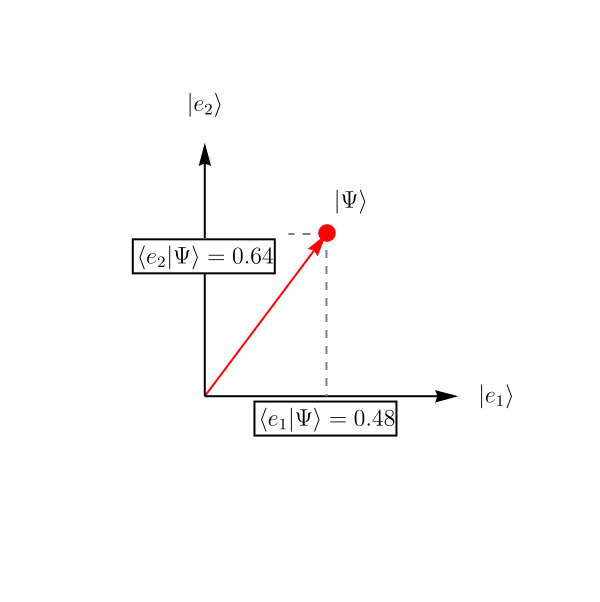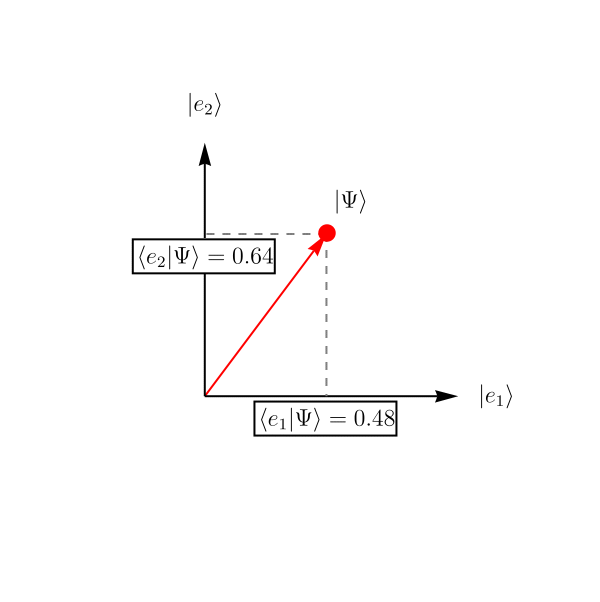
正規直交完全系 (= 長さが1で、自分以外との内積が0で、どんなベクトルでも展開できる基底たち) \(\left\{ \left| e_1 \right>, \left| e_2 \right> \right\}\) があるとしよう。 ベクトル \(\left| \Psi \right>\) を、係数 \(c_1, c_2\) を用いて \[ \left| \Psi \right> = c_1 \left| e_1 \right> + c_2 \left| e_2 \right>, \] と展開できる。 係数 \(c_1, c_2\) は、\(\left| \Psi \right>\) と \(\left| e_1 \right>\) あるいは \(\left| \Psi \right>\) と \( \left| e_2 \right>\) の内積を取ってやれば、 \[ c_1 = \left< e_1 | \Psi \right>, \qquad \\ c_2 = \left< e_2 | \Psi \right>, \] と求めることができる。 この様子を示したのが下図である。 この基底を取った人にとっては、ベクトル \(\left| \Psi \right>\) は \[ \left| \Psi \right> \overset{表示}{=} \left( \begin{array}{c} 0.48 \\ 0.64 \end{array} \right), \] と見えている。 少し別の言い方をすれば、\( \left| \Psi \right> \) の中に \( \left| e_1 \right> \) が \( \left< e_1 | \Psi \right> = 0.48 \) だけ、\( \left| e_2 \right> \) が \( \left< e_2 | \Psi \right> = 0.64 \) だけ存在する、ということである。
しかし、物の見方というのはいくつもある。 別の正規直交完全系 \(\left\{ \left| e'_1 \right>, \left| e'_2 \right> \right\}\) を使いたい人もいるだろう。 その人にとって \(\left| \Psi \right>\) は \[ \left| \Psi \right> = c'_1 \left| e'_1 \right> + c'_2 \left| e'_2 \right>, \] であり、係数 \(c'_1, c'_2\) は先程と同じように \[ c'_1 = \left< e'_1 | \Psi \right>, \qquad \\ c'_2 = \left< e'_2 | \Psi \right>, \] で与えられる。 この様子を示したのが下図である。 この基底を取った人にとっては、ベクトル \(\left| \Psi \right>\) は \[ \left| \Psi \right> \overset{表示}{=} \left( \begin{array}{c} 0.69 \\ 0.40 \end{array} \right), \] と見えている。 ベクトル \( \left| \Psi \right> \) 自身は全く変わっていないことに注意してほしい。 先程と同じ言い方をすれば、\( \left| \Psi \right> \) の中に \( \left| e'_1 \right> \) が \( \left< e'_1 | \Psi \right> = 0.69 \) だけ、\( \left| e'_2 \right> \) が \( \left< e'_2 | \Psi \right> = 0.40 \) だけ存在する、ということである。

4-2. 波動関数とは
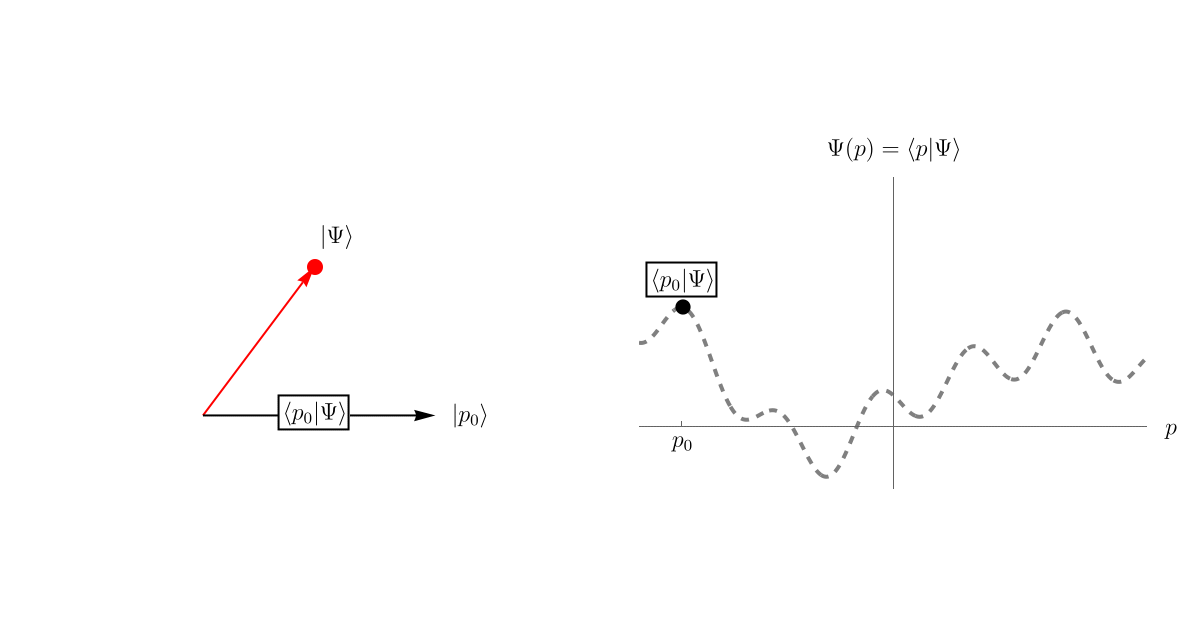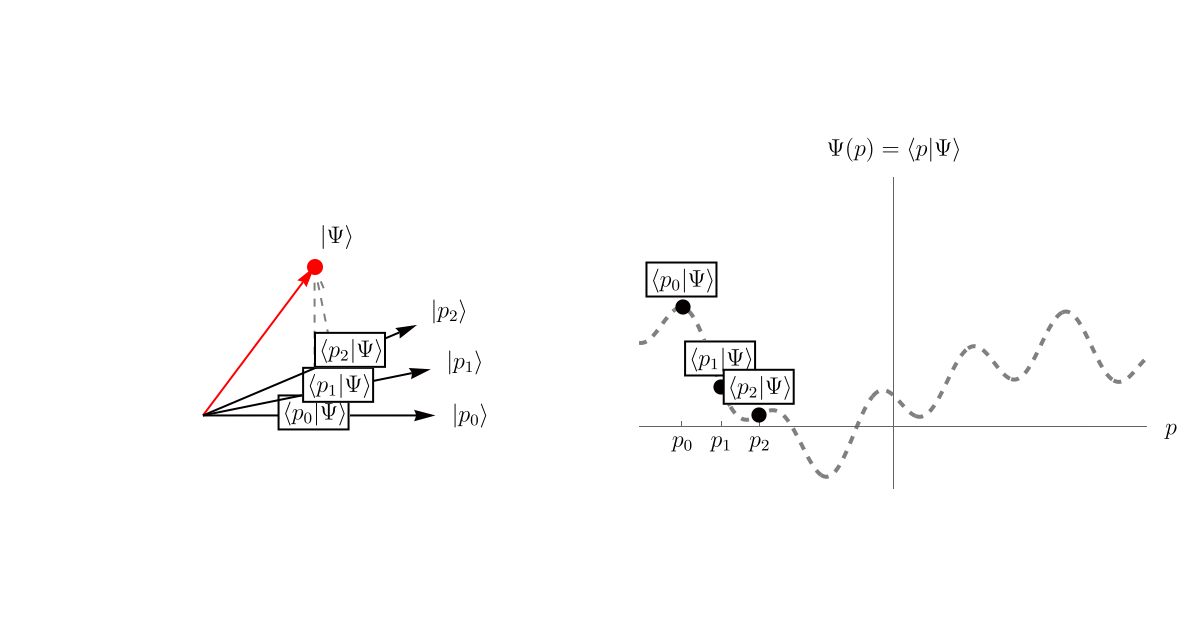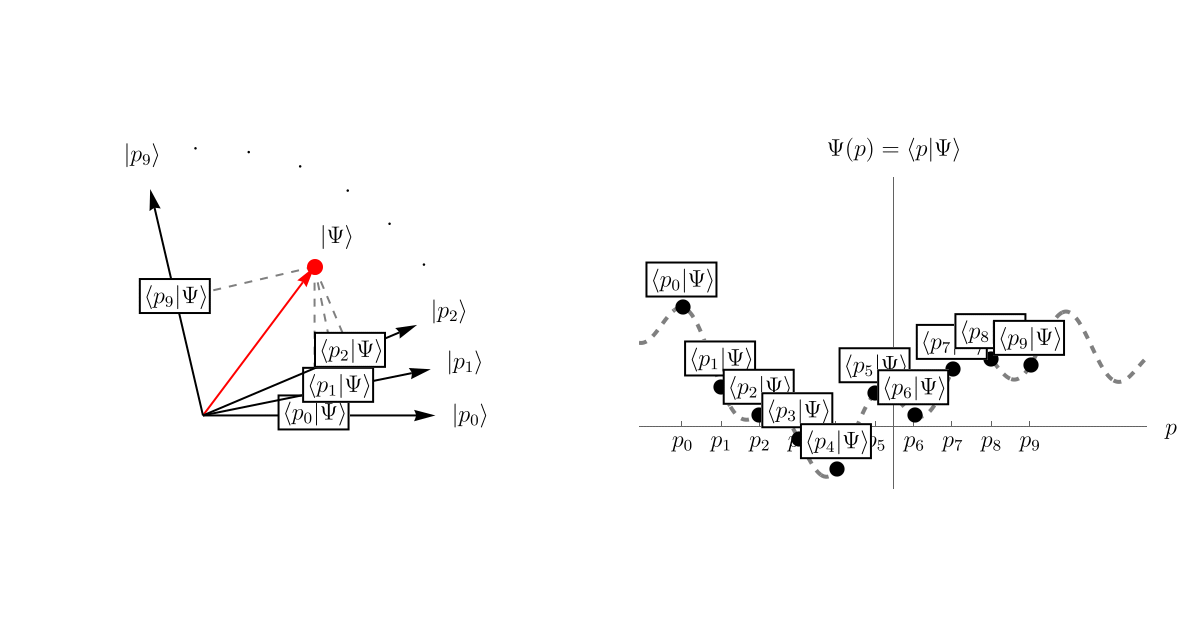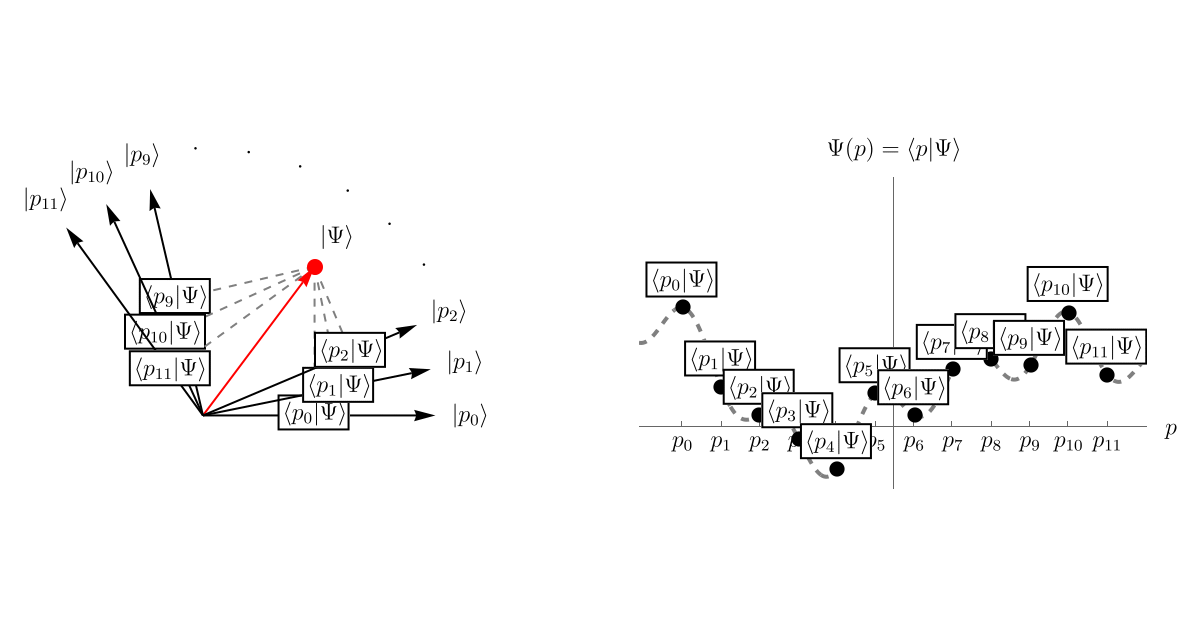
さて、我々は前回まで波動関数 \( \Psi (t, x) \) をひたすら計算してきたわけだが、あれは一体何だったのだろうか。 いきなり答えを言おう。 まず、「系の状態」というのは何らかの抽象的なベクトルで表されるとする。 それを \[ \left| \Psi \right> \] としよう。 位置 \( x \) が引数に入っていないことからわかる通り、これは \( x \) とは関係ない概念である。 空間が1次元や3次元だからといって \( \left| \Psi \right> \) が1次元だったり3次元だったりするわけではない。 \( \left| \Psi \right> \) はあくまで抽象的なベクトルである。
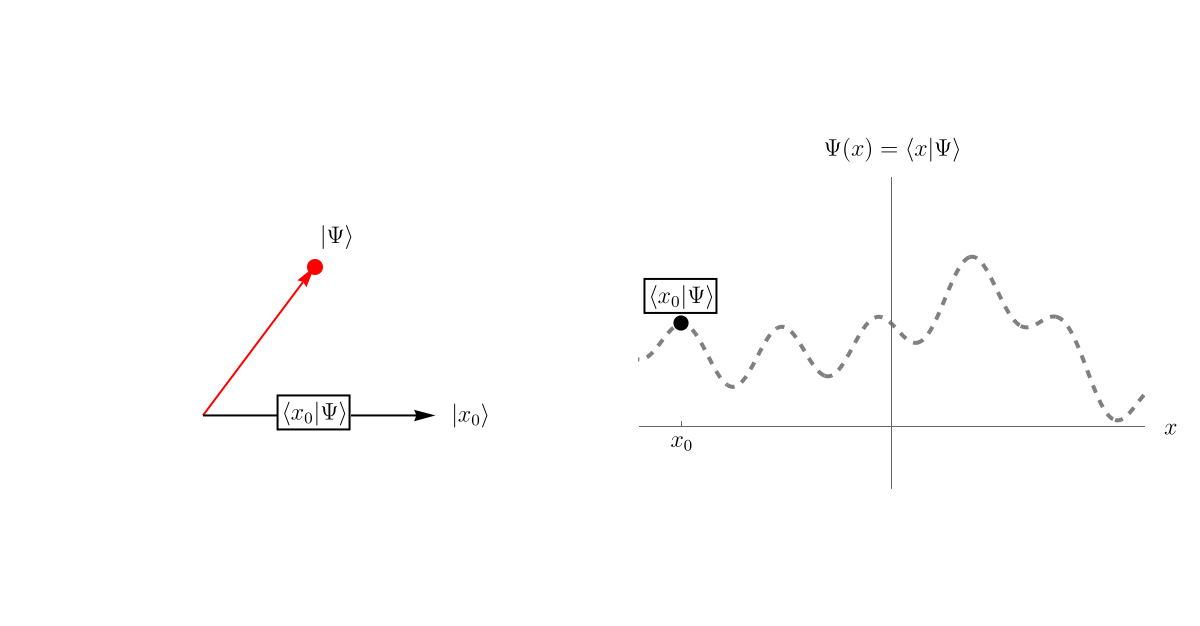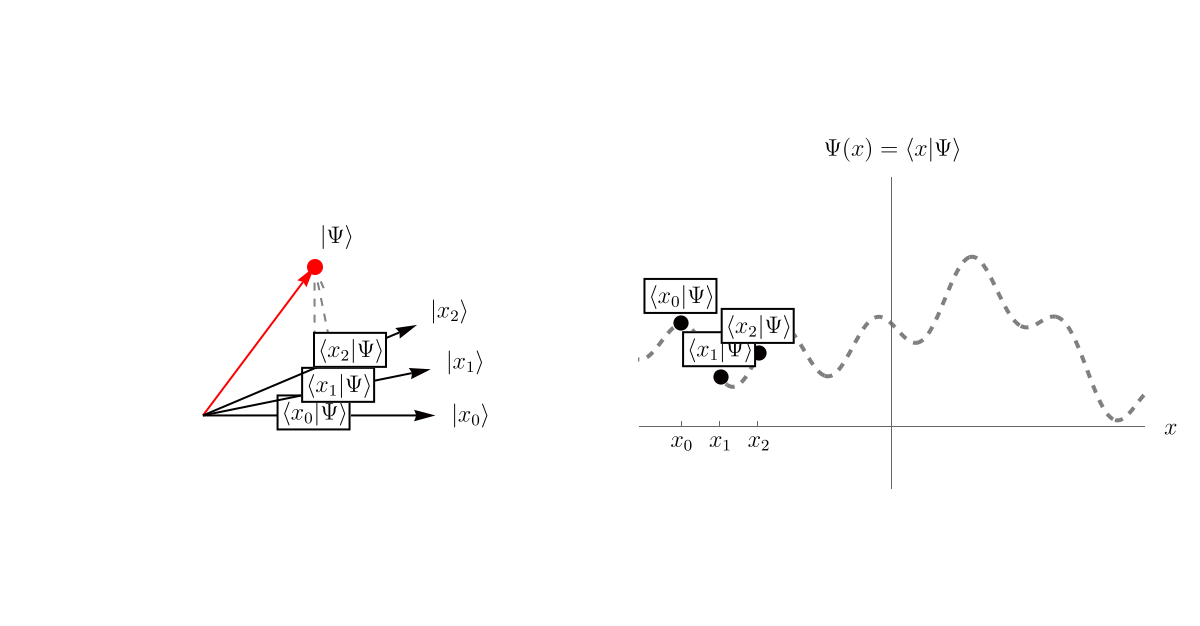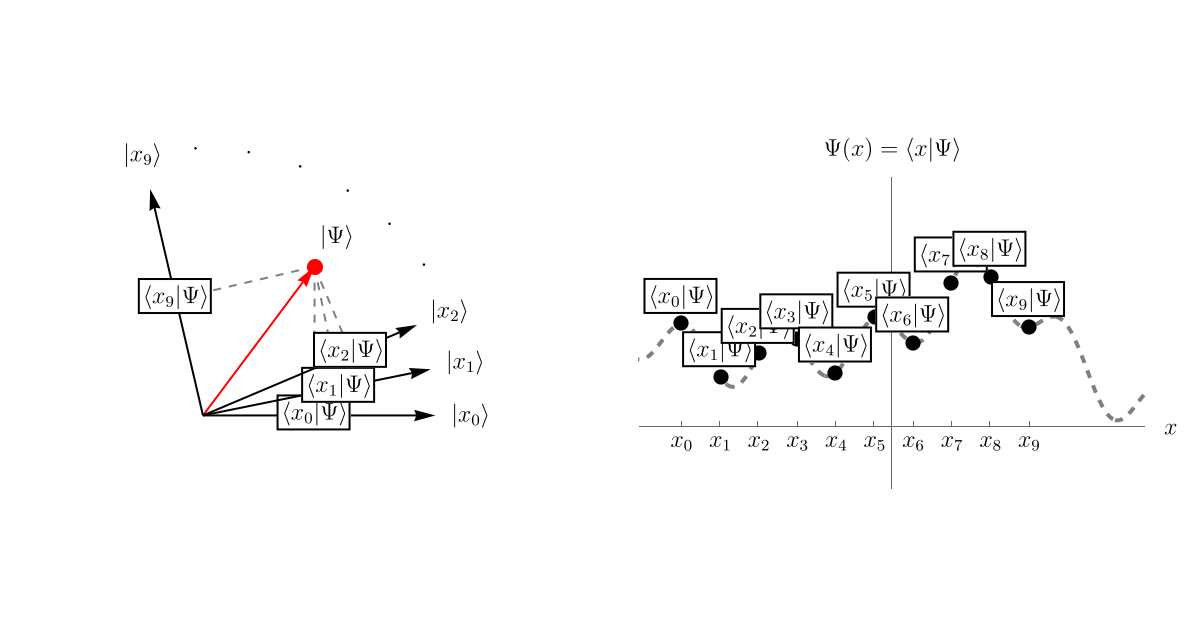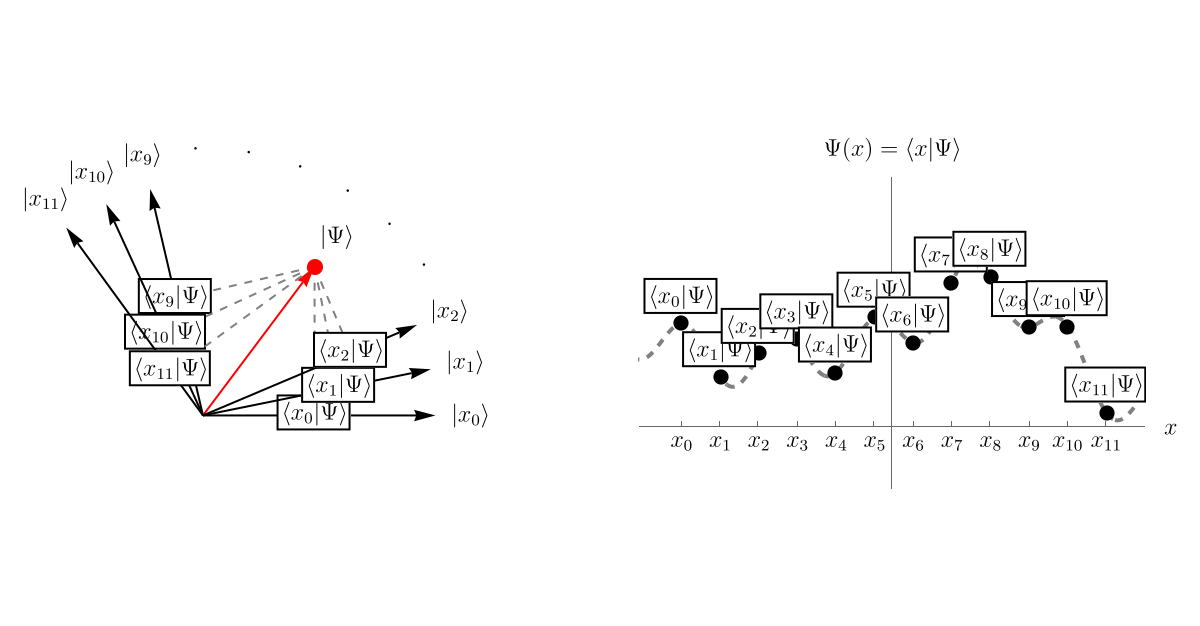
次に、この \( \left| \Psi \right> \) を表示するための基底を用意する。 そのために無限個のベクトル \( \left\{ \left| x \right> \right\} \) を用意しよう。 無限個だからといって心配する必要はない。 空間を細かく区切って \( \left\{ \cdots, x_{- 1}, x_0, x_1, x_2, \cdots \right\} \) とし、それぞれの位置に対応するベクトル \( \left\{ \cdots, \left| x_{- 1} \right>, \left| x_0 \right>, \left| x_1 \right>, \left| x_2 \right>, \cdots \right\} \) を用意したと思えば良い。 これらはお互いに直交しているとする。
そして、波動関数 \( \Psi (t, x) \) というのは、\( \left| \Psi \right> \) を基底 \( \left\{ \left| x \right> \right\} \) で表示したときの係数 \( \left< x | \Psi \right> \) である。 先程までと同じ言い方をすれば、波動関数 \( \Psi (t, x) = \left< x | \Psi \right> \) とは \( \left| \Psi \right> \) の中に \( \left| x \right> \) がどれだけ存在するかである。 以下のアニメーションを見てほしい。 直交するベクトルが無限個あるので表示しきれないが、それぞれの \( \left| x_i \right>, \left| x_j \right>~(i \neq j)\) は直交している。 そして、\( \left| \Psi \right> \) の中にどれくらい \( \left| x \right> \) があるかを \( \left< x | \Psi \right> \) で見積もることができる。 これが波動関数 \( \Psi (t, x) \) である。
時間依存性はどこに行ったのか?と思うかもしれない。 実は、\( \left| \Psi \right> \) は抽象的なベクトル空間の中で \[ \left| \Psi (t) \right> \] と時間発展をしている。 この時間発展を記述するのがSchrödinger方程式である。 これについては次回学ぶことにしよう。
ところで、基底の取り方には任意性があった。 別に \( \left\{ \left| x \right> \right\} \) を選ぶ必要はないのである。 例えば、運動量 \( \left\{ \left| p \right> \right\} \) を基底に選んでも良い。 そうすると、運動量表示の波動関数 \( \Psi (t, p) = \left< p | \Psi \right> \) を得ることができる。 これは一番初めの例で基底を \( \{ \left| e_1 \right>, \left| e_2 \right> \} \) と選んでも \( \{ \left| e'_1 \right>, \left| e'_2 \right> \} \) と選んでも良いことに対応している。
(おまけ) Fourier変換のこころ
Fourier変換よりも少し簡単な例で考えてみよう。 例えば次の図のような関数があったとする。
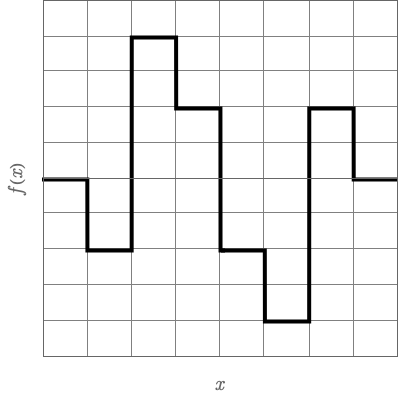
この関数形を他の人に伝えるにはどうしたらいいだろうか。 一番素直には、それぞれの \(x\) でこの関数がどういう値を持つか、逐一伝えればよい。 今の場合、\(x = 1, 2, 3, 4, 5, 6, 7, 8\) で \(f (x) = 0, -2, 4, 2, -2, -4, 2, 0\) である。
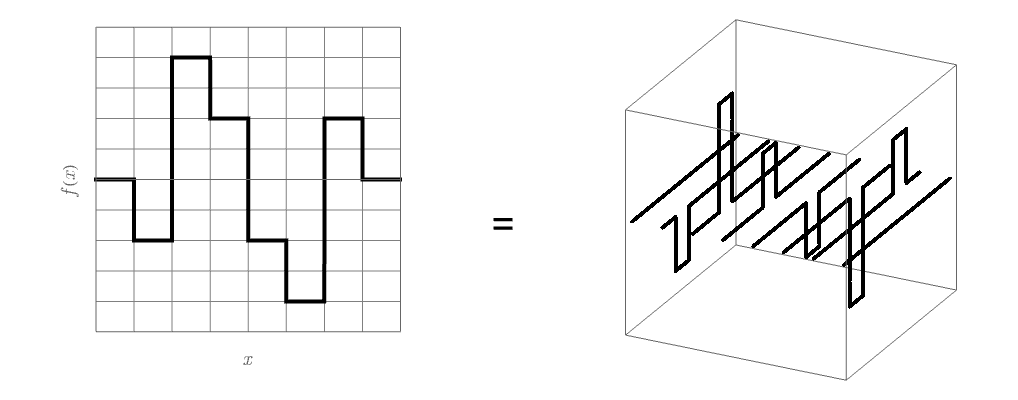
実は別の方法がある。 異なる波数 \(k\) の波が何個あるかで伝える方法である。
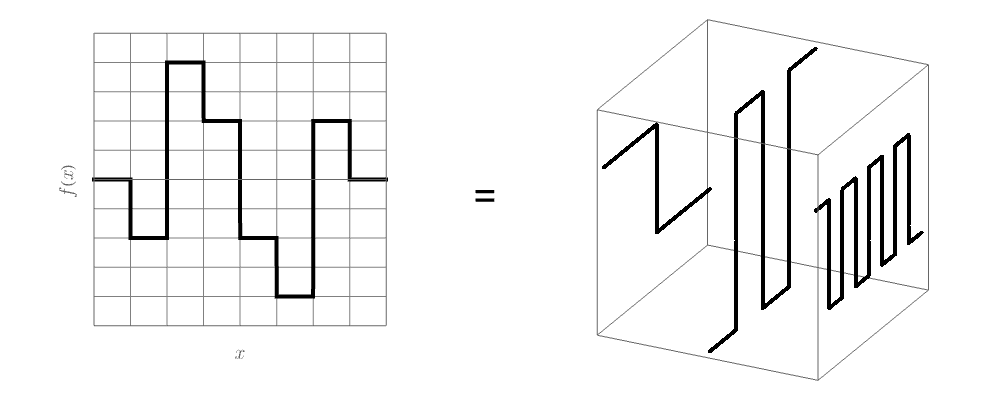
どちらの伝え方でも相手には同じ情報が伝わる。 Fourier変換の考え方も基本的に同じである。 \(f (x)\) を各 \(x\) の値に対する \(f (x)\) の値の集まりとして表してもいいし、波数 \(k\) の波 \(e^{i k x}\) が各 \(k\) についてどれくらいあるかで表してもいい。 \(f (x)\) に \(e^{i k x}\) がどれくらいあるかを表す量である \(\tilde{f} (k)\) は、その複素共役 \(e^{- i k x}\) で \(f (x)\) に「問い合わせ」るとわかる \[ \tilde{f} (k) = \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^\infty dx~f(x) e^{- i k x}. \] 元の \(f (x)\) は、波 \(e^{i k x}\) にその存在量 \(\tilde{f} (k)\) を掛けて、\(k\) について足し合わせれば再現できる \[ f (x) = \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^\infty dk~\tilde{f}(k) e^{i k x}. \]
(おまけ) Fourier変換の例
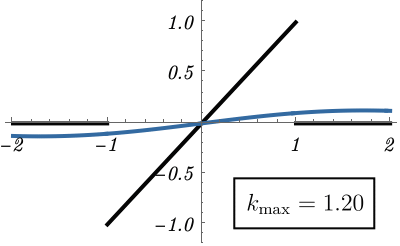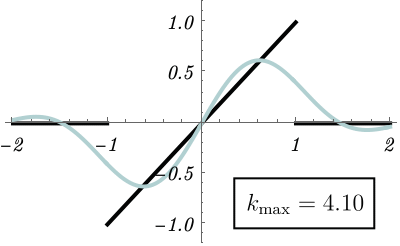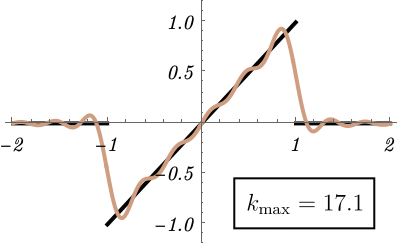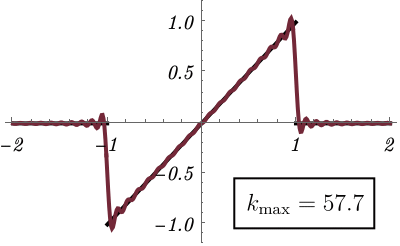
上の説明だけだと抽象的なので、具体例を見てみよう。 関数 \(f (x)\) を \[ f (x) = \left\{ \begin{matrix} x & (- 1 < x < 1) \\ 0 & {\rm (otherwise)} \end{matrix} \right. , \] としよう。 これは下図の黒線で、不連続点があるのがわかる。 こんな非自明な関数をFourier変換は再現できるのだろうか。 実はこの例では \(\tilde{f} (k)\) を解析的に求めることができる \[ \tilde{f} (k) = \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^\infty dx~f(x) e^{- i k x} = \cdots = i \sqrt{\frac{2}{\pi}} \frac{k \cos k - \sin k}{k^2}. \] これが「\(f (x)\) の中に \(e^{i k x}\) がどれくらいあるか」である。 元の関数を再現する様子を見るために、積分範囲を \(k \in [- k_{\rm max}, k_{\rm max}]\) として、 \[ \tilde{\tilde{f}} (x) = \frac{1}{\sqrt{2 \pi}} \int_{- k_{\rm max}}^{k_{\rm max}} dk~\tilde{f}(k) e^{i k x}, \] が \( k_{\rm max} \to \infty \) でもとの関数になるかどうか調べてみよう。 下図は \(k_{\rm max}\) を大きくしたときの \(\tilde{\tilde{f}} (x)\) の振る舞いである。 \(k_{\rm max}\) が大きくなるにつれて元の関数 \(f (x)\) が再現されていく様子がわかる。