Materials
今回も引き続き、時間に依存しないSchrödinger方程式 \[ H \psi_n (x) = E_n \psi_n (x), \] について学ぶ。 束縛状態と散乱状態がどちらも現れるようなポテンシャルについて以下で見る。
3-1. デルタ関数井戸
デルタ関数井戸
\[ V (x) = - \alpha \delta (x) \quad (\alpha > 0) \]
における、時間に依存しないSchrödinger方程式のエネルギー固有状態 \(\psi_n (x)\) の時間発展 \(\Psi_n (t, x) = \psi_n (x) \varphi_n (t)\) を図に示してある。
青線・黄線・緑線はそれぞれ \({\rm Re} \Psi (t, x), {\rm Im} \Psi (t, x), |\Psi (t, x)|^2\) である。
デルタ関数については、以下の(おまけ)も参照。
重要なことは、束縛状態(左)と散乱状態(右)がどちらも現れることである。
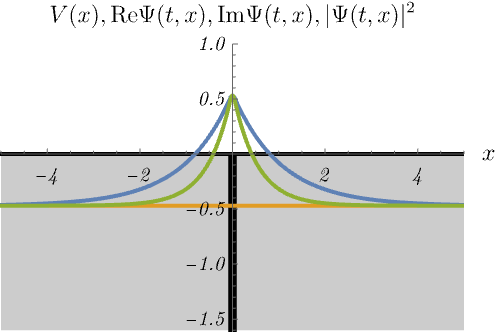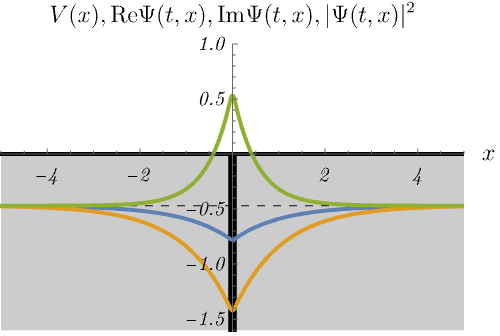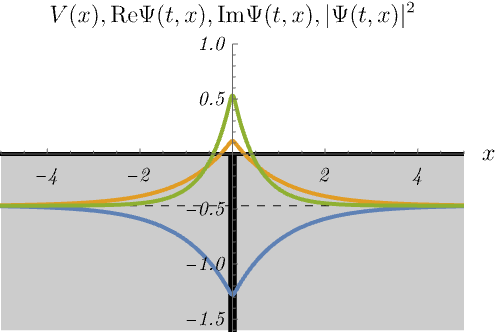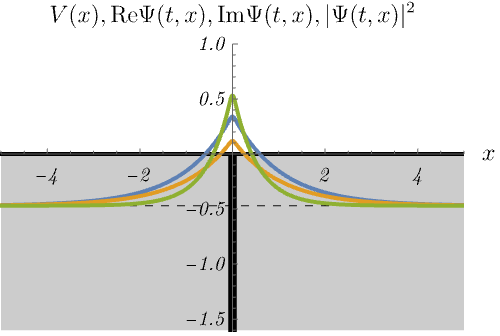
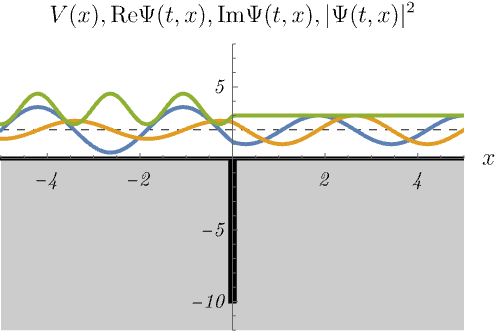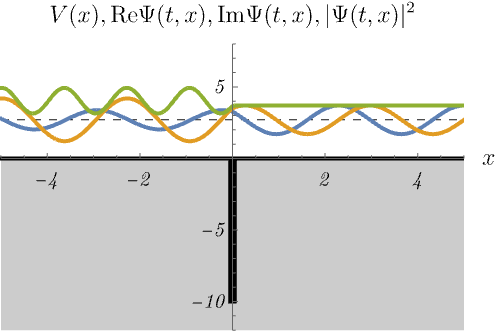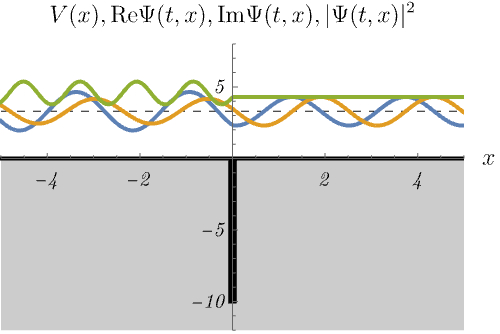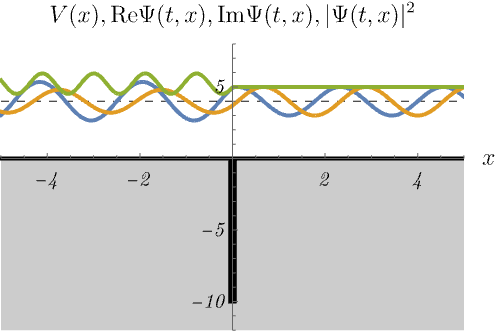
束縛状態と散乱状態の最も大きな違いは、エネルギー固有値が離散的か連続的かである。 左図は束縛状態なので、\(E\) の値が特別でないと波動関数が \(x \to \pm \infty\) で発散してしまう。 したがって、波動関数が有限であるためには、\(E_n\) のラベル \(n\) は離散的な値しか取ることができない。 これは前回の無限井戸型ポテンシャルや調和振動子と似た振る舞いである。 一方右図は散乱状態なので、\(E\) の値を少し変えても時間に依存しないSchrödinger方程式は有限の解を持つ。 つまり \(E_n\) のラベル \(n\) は連続的に変化できる。 これは前回の平面波と似た振る舞いである。 右図ではエネルギーを少しずつ変えたときに解が存在し続ける様子を示している。 また、右図で \(|\Psi (t, x)|^2\) が左側だけ波打っているのは、入射波と反射波の干渉による。
3-2. デルタ関数障壁
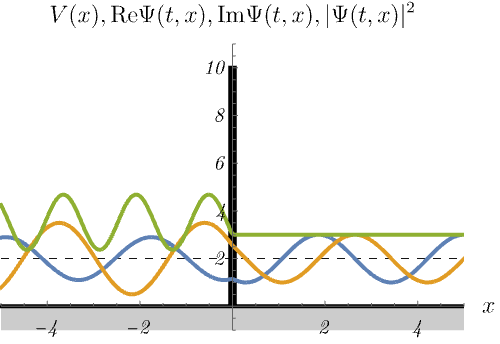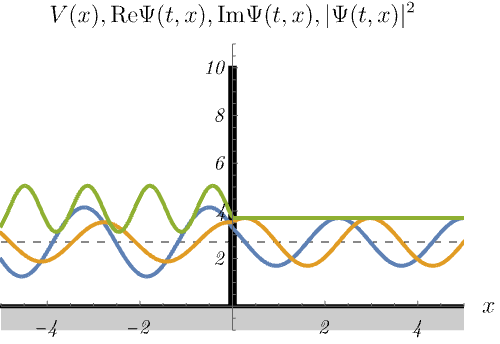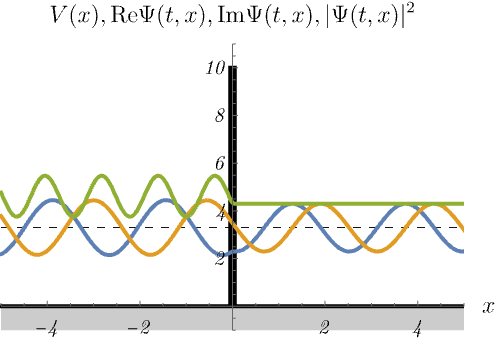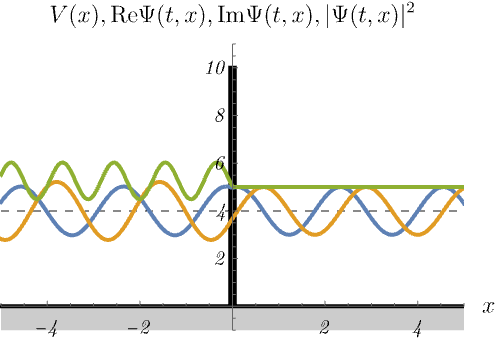
デルタ関数障壁
\[ V (x) = \alpha \delta (x) \quad (\alpha > 0) \]
における、時間に依存しないSchrödinger方程式のエネルギー固有状態 \(\psi_n (x)\) の時間発展 \(\Psi_n (t, x) = \psi_n (x) \varphi_n (t)\) を図に示してある。
青線・黄線・緑線はそれぞれ \({\rm Re} \Psi (t, x), {\rm Im} \Psi (t, x), |\Psi (t, x)|^2\) である。
デルタ関数井戸の場合と異なり、散乱状態しか現れない。
\(|\Psi (t, x)|^2\) が左側だけ波打っているのは、入射波と反射波の干渉による。
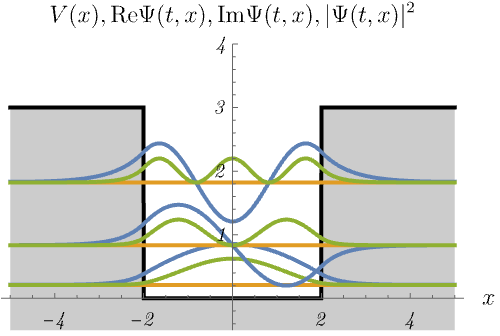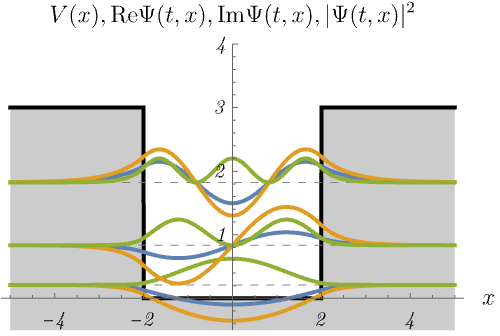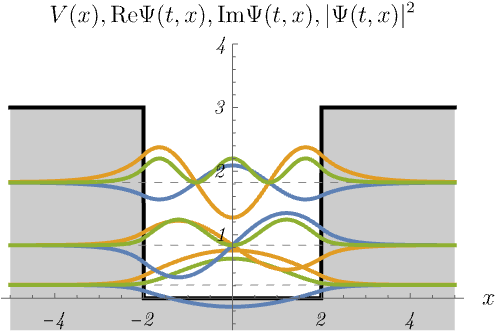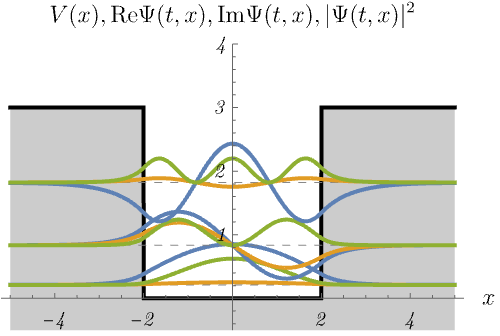
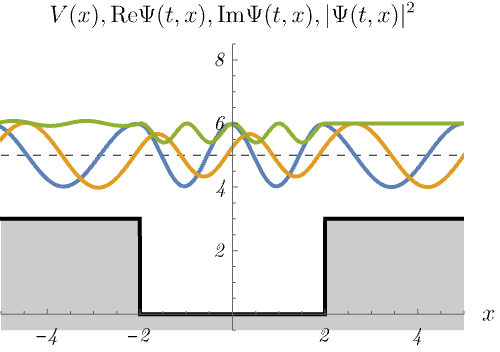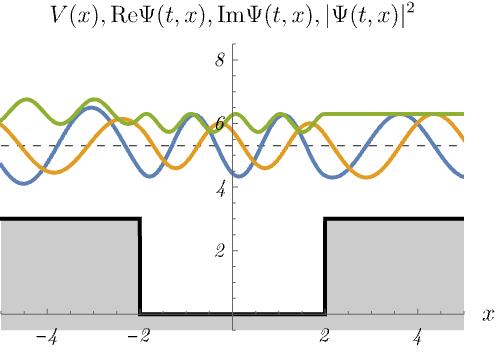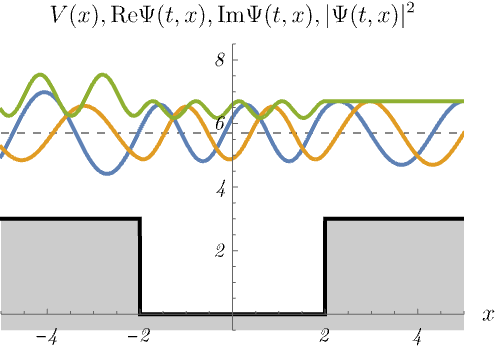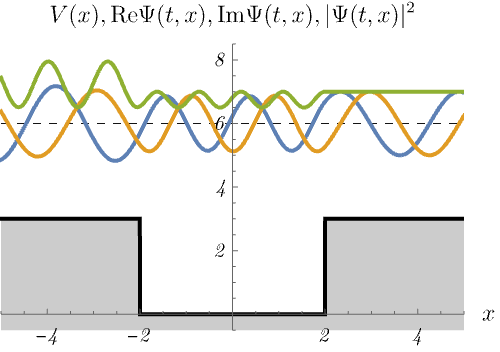
3-3. 有限井戸型ポテンシャル
有限井戸型ポテンシャル
\[ V (x) = \left\{ \begin{matrix} 0 & (- 2 < x < 2) \\ 3 & ({\rm otherwise}) \end{matrix} \right. \]
における、時間に依存しないSchrödinger方程式のエネルギー固有状態 \(\psi_n (x)\) の時間発展 \(\Psi_n (t, x) = \psi_n (x) \varphi_n (t)\) を図に示してある。
青線・黄線・緑線はそれぞれ \({\rm Re} \Psi (t, x), {\rm Im} \Psi (t, x), |\Psi (t, x)|^2\) である。
デルタ関数井戸の場合と同じく、束縛状態(左)と散乱状態(右)が現れる。
(おまけ) デルタ関数
デルタ関数というのは、次の性質を満たす関数のことである
\[ \int_{- \infty}^\infty dx~\delta (x) = 1, \]
\[ \int_{- \infty}^\infty dx~f(x)~\delta (x - a) = f(a). \]
これを理解するため、極限的にデルタ関数 \(\delta (x)\) になる3つの関数の振る舞いを見てみよう。
\[ \delta_1 (x) = \left\{ \begin{matrix} \frac{1}{2 a} & (- a < x < a) \\ 0 & {\rm (otherwise)} \end{matrix} \right., \qquad \delta_2 (x) = \frac{1}{\sqrt{2 \pi a^2}} e^{- \frac{x^2}{2 a^2}}, \qquad \delta_3 (x) = \frac{\sin (x / a)}{\pi x} \]
いずれも
\[ \int_{- \infty}^\infty dx~\delta_i (x) = 1 \quad (i = 1, 2, 3)\]
より、1つ目の性質を満たしている。
図の青線・黄線・緑線はそれぞれ \(\delta_1 (x), \delta_2 (x), \delta_3 (x)\) の \(a\) を変えたときの振る舞いである。
\(a \to 0\) でいずれも原点に鋭いピークを作ることがわかる。
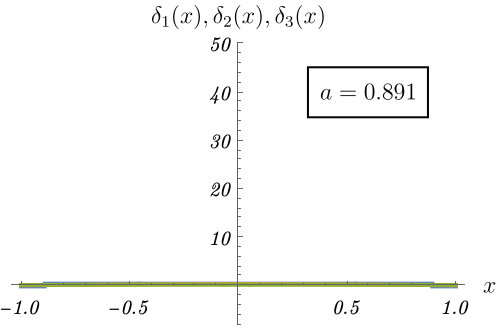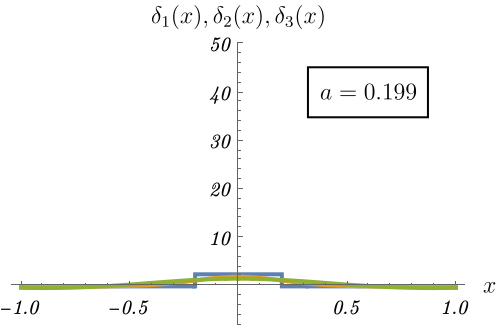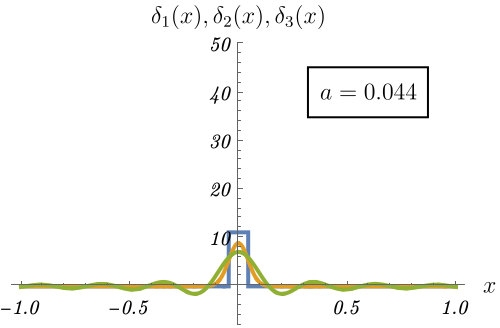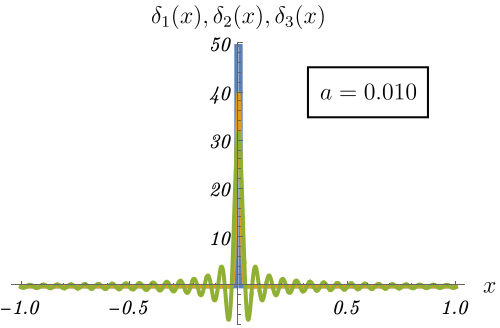
この極限で \(x = 0\) 周りしか積分に寄与しなくなるため、デルタ関数の満たすべき性質 \[ \int_{- \infty}^\infty dx~f (x) \delta (x - a) = f (a) \] が実現される。
(おまけ) 束縛状態と散乱状態
エネルギー \(E\) がポテンシャル \(V (x)\) を超えているか超えていないかで散乱状態か束縛状態が決まるのであった。
\(x \to \pm \infty\) でどちらも \(E < V (x)\) となっていれば束縛状態、そうでなければ散乱状態である。
無限井戸型ポテンシャルや調和振動子の場合は束縛状態のみ、デルタ関数障壁の場合は散乱状態のみである一方、デルタ関数井戸や有限井戸型ポテンシャルの場合はどちらの状態も現れた。
ところで、次の図は束縛状態だろうか、散乱状態だろうか。
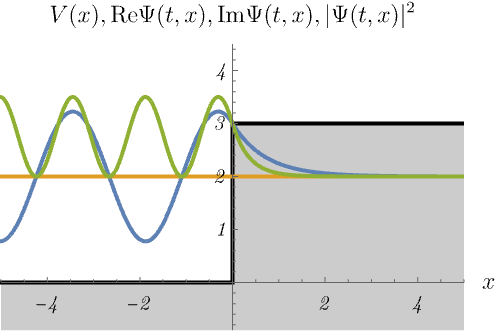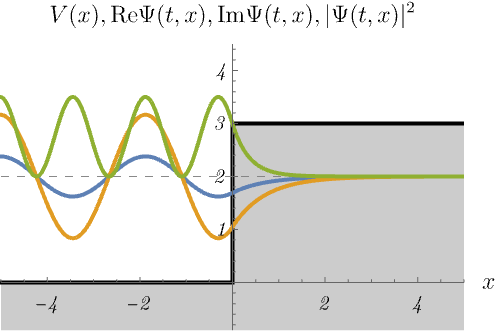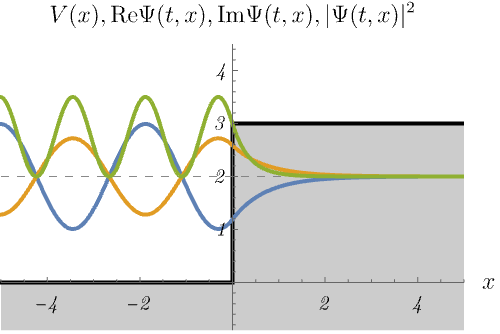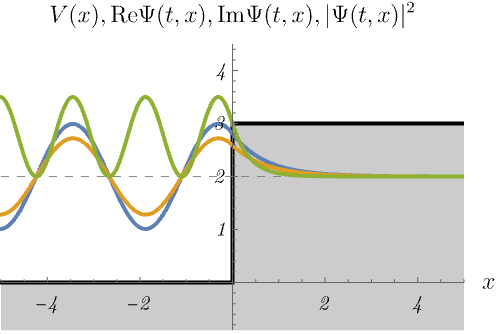
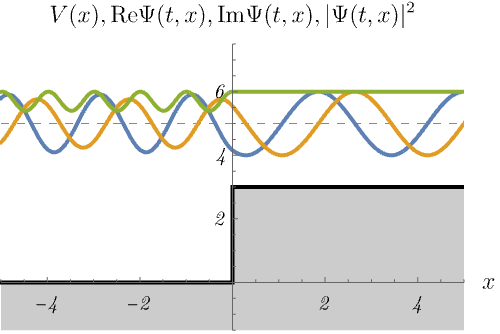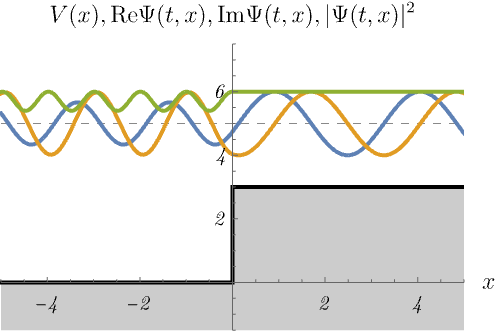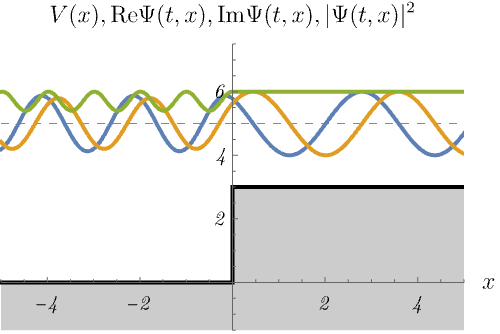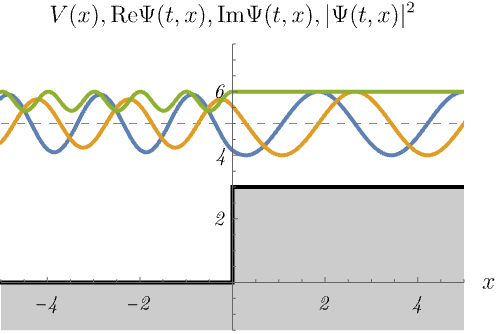
右図が散乱状態であることはわかりやすいが、左図も \(E > V (x \to - \infty)\) であるため散乱状態であることに注意してほしい。 右図では、左からやってきた波がポテンシャルによって波数を変えながら右へ透過していく様子が見える。 確率密度が \(x < 0\) で波打っているのは、入射波とわずかな反射波の干渉のためである。 一方、左図ではエネルギーが足りないため波動関数が透過できない。 結果、入射波は全て反射され、\(x < 0\) で入射波との干渉により定在波ができる。 また、波動関数は透過できないものの、\(x > 0\) の領域に染み出していることもわかる。