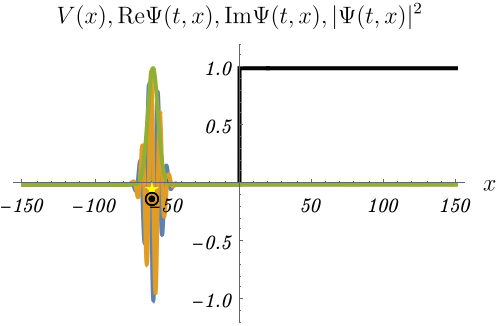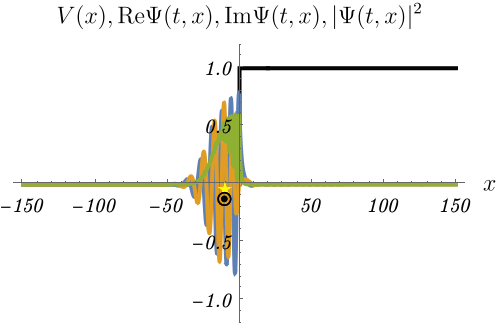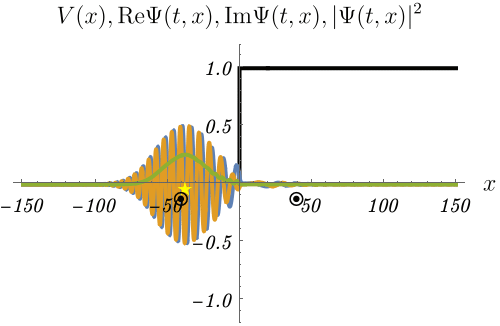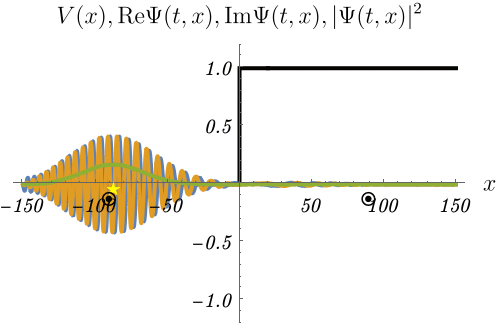Materials
今回は時間に依存するSchrödinger方程式 \[ i \hbar \frac{\partial}{\partial t} \Psi (t, x) = H \Psi (t, x), \qquad H = - \frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2} + V (x), \] をうまく解く方法について学ぶ。 その方法とは、\(\Psi (t, x)\) をより簡単な構成要素 \(\Psi_n (t, x) = \psi_n (x) \varphi_n (t)\)の線型結合 \[ \Psi (t, x) = \sum_n c_n \Psi_n (t, x), \] として表す方法である。 この構成要素のうち、\(\psi_n (x)\) を求める方程式が、時間に依存しないSchrödinger方程式 \[ H \psi_n (x) = E_n \psi_n (x), \] である。 エネルギー固有値 \(E_n\) が求まると、時間発展は \(\varphi_n (t) = e^{- i E_n t / \hbar}\) と決まる。
2-1. 無限井戸型ポテンシャル
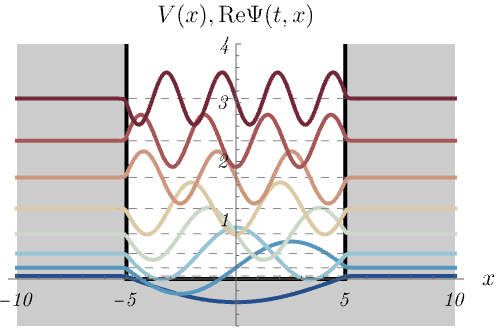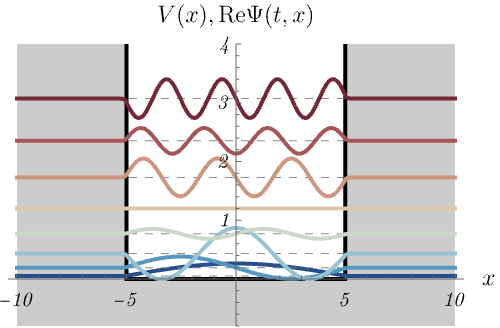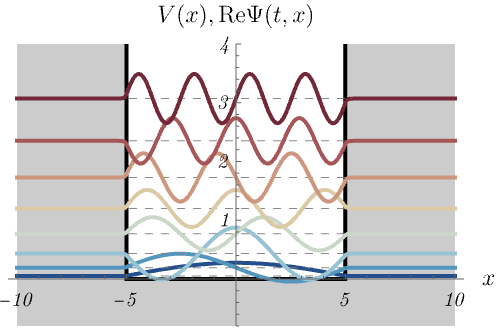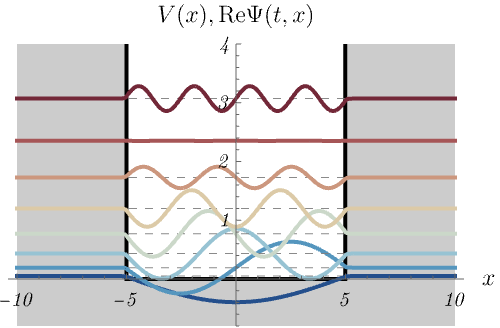
無限井戸型ポテンシャル
\[ V (x) = \left\{ \begin{matrix} 0 & (- 5 < x < 5) \\ \infty & ({\rm otherwise}) \end{matrix} \right., \]
における、時間に依存しないSchrödinger方程式のエネルギー固有状態 \(\psi_n (x)\) の時間発展 \(\Psi_n (t, x) = \psi_n (x) \varphi_n (t)\) を図に示してある。
\(\Psi_n (t, x)\) は確率密度が時間によらず一定になるので、定常状態とも呼ばれる。
1つの図にポテンシャル \(V (x)\) と波動関数 \(\Psi_n (t, x)\) の実部が同時に示されているので注意してほしい。
波動関数については原点をエネルギー \(E_n\) だけ上方向にシフトしてある。
\(E_n\) が大きいほど振動が速い様子が見えるだろうか。
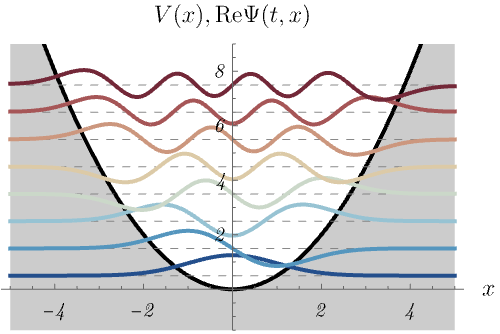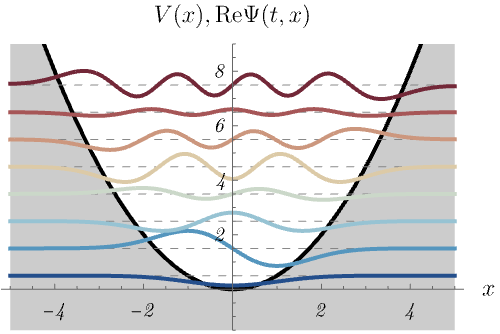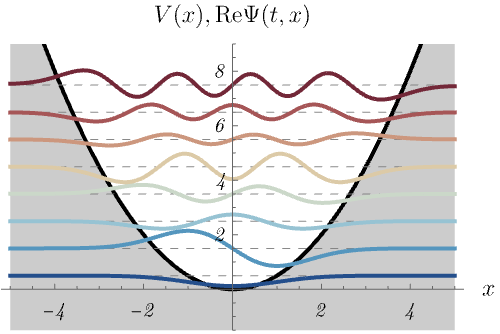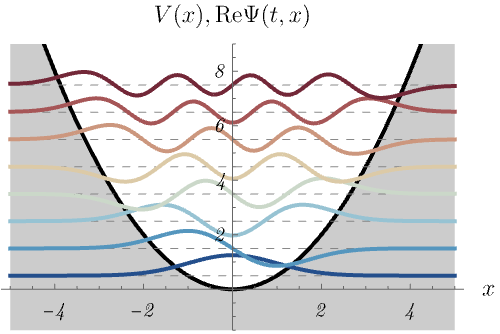
2-2. 調和振動子
調和振動子ポテンシャル
\[ V (x) = \frac{1}{2} m \omega^2 x^2, \]
における、時間に依存しないSchrödinger方程式のエネルギー固有状態 \(\psi_n (x)\) の時間発展 \(\Psi_n (t, x) = \psi_n (x) \varphi_n (t)\) を図に示してある。
1つの図にポテンシャル \(V (x)\) と波動関数 \(\Psi_n (t, x)\) の実部が同時に示されている。
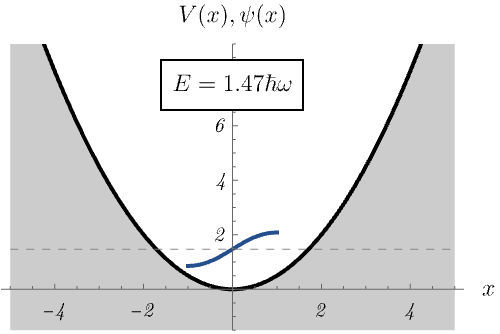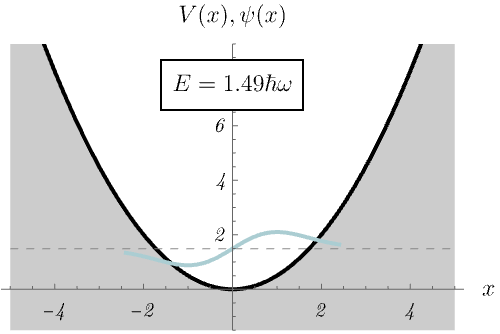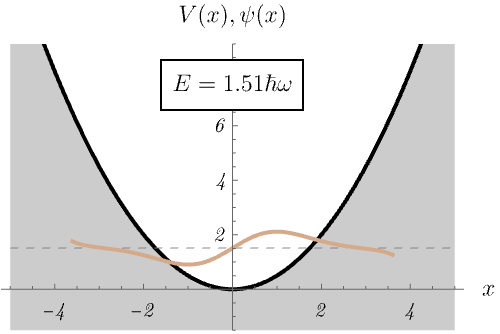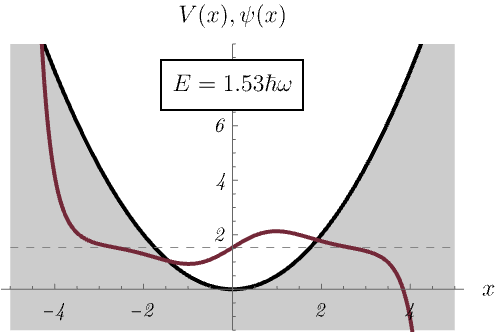
ところで、なぜエネルギー固有値 \(E_n\) が離散的になるのだろうか。 下図では、\(E_n\) の値を無理やり変えたとき、時間に依存しないSchrödinger方程式の解の振る舞いがどう変わるか示している。 \(E_n\) の値が絶妙でないと波動関数が発散してしまうのがわかるだろうか。 許される \(E_n\) の値が離散化されるのは、発散しない波動関数が存在するという条件による。
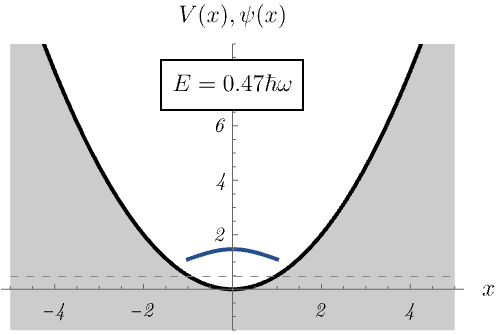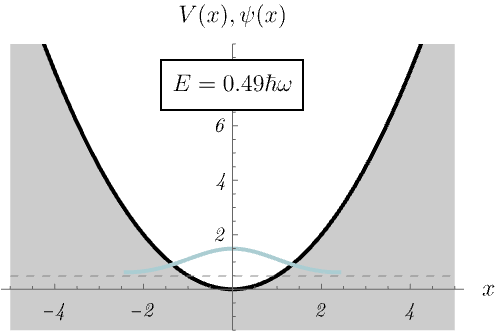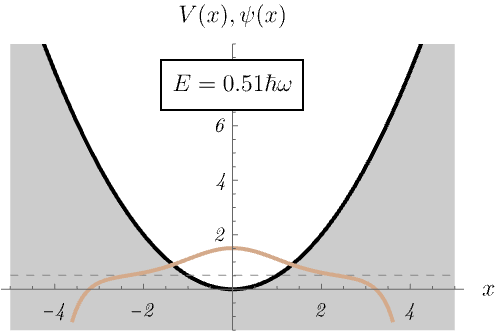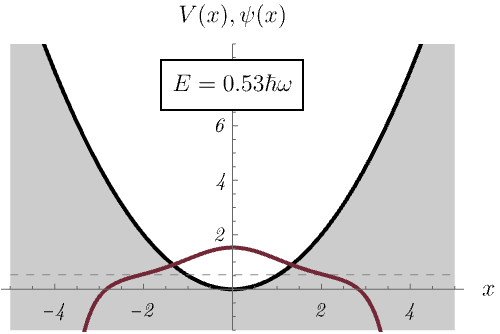
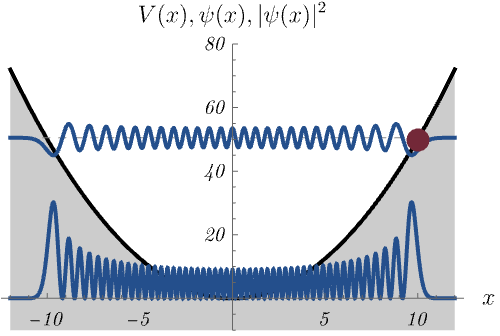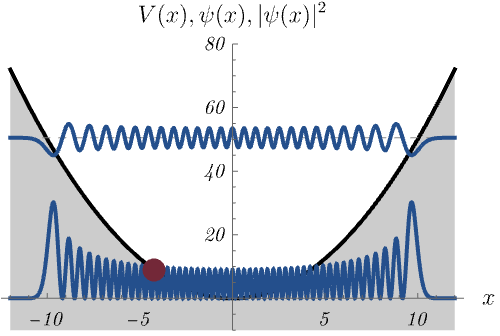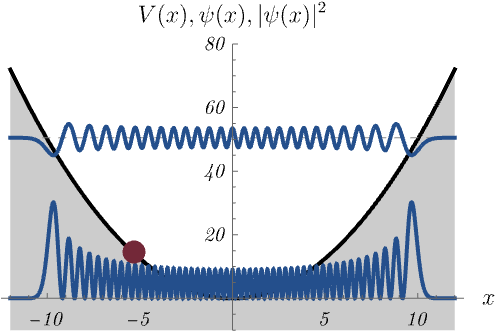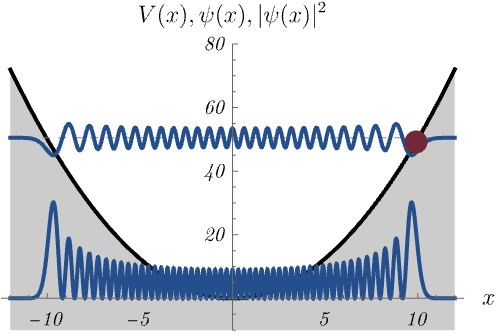
この量子力学的な調和振動子は、古典的な調和振動子(= ばね)とどう関係するのだろうか。 下図は、比較的高いエネルギー準位 \(E_n = \left( 50 + \frac{1}{2} \right) \hbar \omega\) に対する波動関数 \(\psi_n (x)\) と確率密度 \(|\psi_n (x)|^2\) を示している。 古典的なばねの運動が古典的転回点 (= 振動の端点) で時間を使いがちなことに対応して、量子力学的な確率密度も古典的転回点で大きくなる。
2-3. 自由粒子ポテンシャル
ポテンシャルが存在しない場合
\[ V (x) = 0, \]
の、時間に依存しないSchrödinger方程式のエネルギー固有状態の時間発展を図に示してある。
これはもちろん平面波 \(\psi_k (x) = e^{i k x}\) の時間発展 \(\Psi_k (t, x) = e^{i (k x - \omega t)}~\left(\omega = \frac{\hbar k^2}{2m}\right)\) である。
無限井戸型ポテンシャルや調和振動子との大きな違いがいくつか存在する。
例えば、波動関数が特定の方向に動いている、波動関数が無限遠まで広がっている、エネルギー固有値が連続的に変化できる、などである。
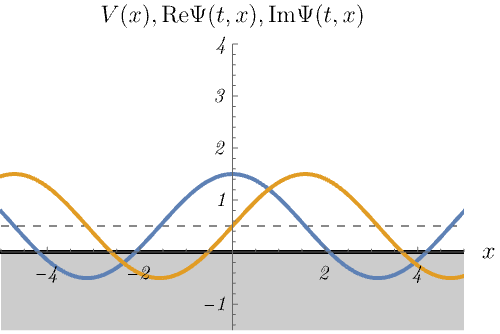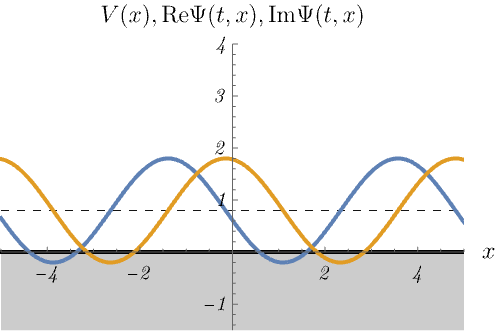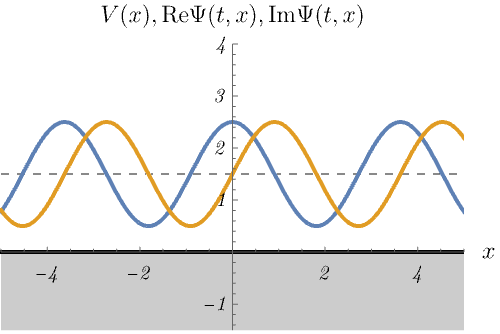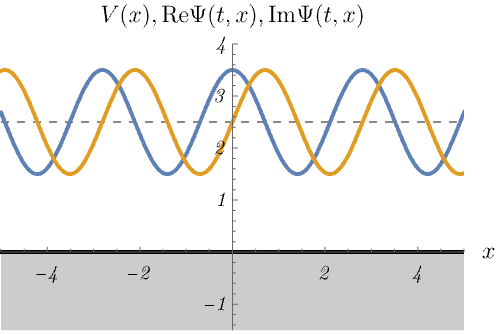
2-3-1. 束縛状態と散乱状態
時間に依存しないSchrödinger方程式のエネルギー固有状態には、束縛状態と散乱状態が存在する。
これを決める条件は、無限遠でエネルギー \(E\) がポテンシャル \(V (x)\) を超えているか超えていないかである。
\(x \to \pm \infty\) でどちらも \(E < V (x)\) となっていれば束縛状態、そうでなければ散乱状態である。
無限井戸型ポテンシャルや調和振動子の場合、無限遠でポテンシャルが発散しているため、束縛状態のみが現れた。
今の場合ポテンシャルが \(V (x) = 0\) なので、\(E > 0\) の状態は散乱状態である。
\(E < 0\) は解が発散するため考える必要がなく、したがって散乱状態のみが現れる。
散乱状態は一般にエネルギー固有値が連続的な値を取る。
2-3-2. 平面波と波束
平面波 \(e^{i k x}\) というのは、無限遠まで広がった波である。
こんなものが現実にあり得るのだろうか?
宇宙の端から端まで広がっている波なんて考えてもしょうがないではないか。
ところが実はそうでもないのである。
\(e^{i k x}\) を \(k\) について適切に足し合わせると、空間的に局在した波を作ることができる。
これを波束と言う。
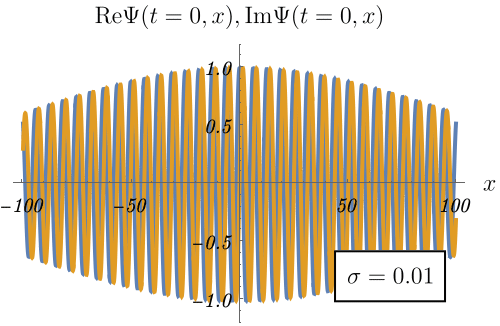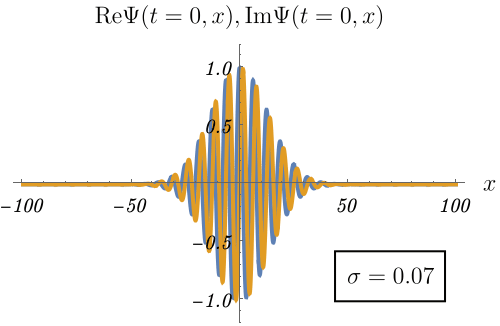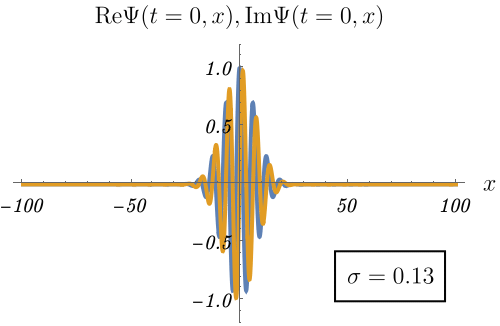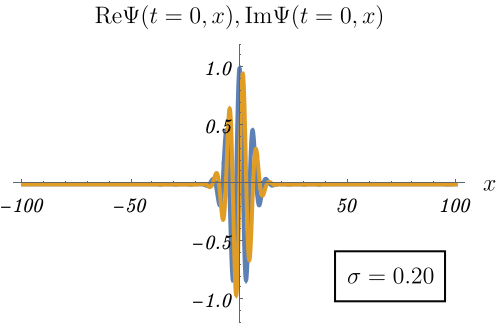
作り方は例えば、
\[ \Psi (t = 0, x) = \int_{- \infty}^\infty dk~c (k) e^{i k x} \]
とし、\(c (k)\) は \(k = k_0\) にピークを持つとする。
\[ c (k) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(k - k_0)^2}{2 \sigma^2}} \]
すると不思議なことに、空間的に局在した波ができる。
下図は \(k_0 = 1\) とした例である。
この波はどう時間発展するだろうか。 Schrödinger方程式は線型方程式で、それぞれの平面波 \(\psi_k (x) = e^{i k x}\) は \( \Psi_k (t, x) = e^{i (k x - \omega t)}~\left(\omega = \frac{\hbar k^2}{2m}\right)\) という時間発展をするので、 \[ \Psi (t, x) = \int_{- \infty}^\infty dk~c (k) \Psi_k (t, x) \] が答えである。 このページの初めに書いた \[ \Psi (t, x) = \sum_n c_n \Psi_n (t, x), \] との類似性に気付いただろうか。 散乱状態の場合は、エネルギー固有値が連続値を取り得ることに対応して、ラベル \(n\) が連続変数に置き換わる。
2-3-3. 位相速度と群速度
上で作った波束の時間発展を見てみよう。
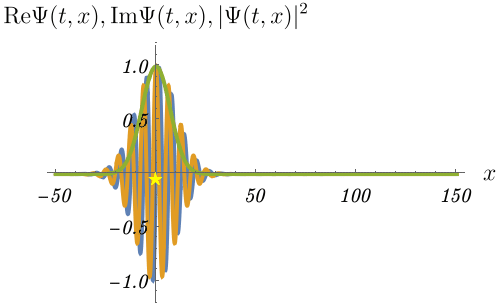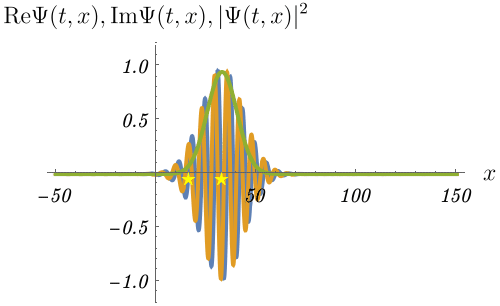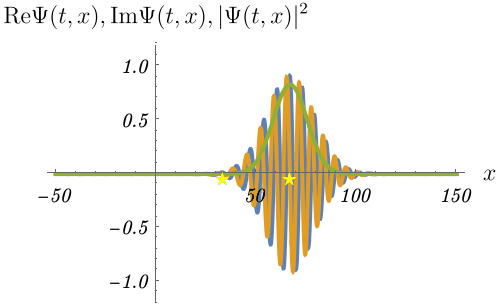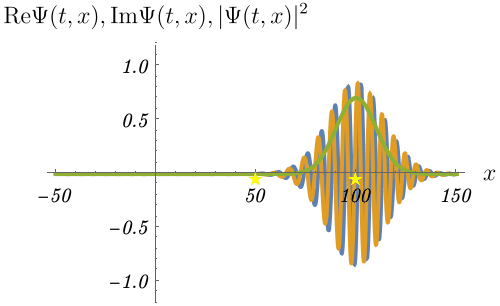
波束の中心 (緑線のピーク) が進む速度と、波束を構成している平面波の位相が一定の地点 (例えば青線のピーク) が進む速度が異なるのがわかるだろうか。 しかも、これらの速度はちょうど2倍だけ異なる。 後者が位相速度、前者が群速度である。 \[ v_{\rm phase} = \frac{\omega}{k} = \frac{\hbar k}{2 m} \] \[ v_{\rm group} = \frac{d\omega}{dk} = \frac{\hbar k}{m} \] 古典的な粒子に対応する速度は波束の中心が伝わる速度なので、群速度である。
(おまけ) 波束の反射
下図は波束
\[ \Psi (t = 0, x) = \int_{- \infty}^\infty dk~c (k) e^{i k x}, \qquad c (k) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(k - k_0)^2}{2 \sigma^2}} \]
が壁で反射される様子を、時間に依存するSchrödinger方程式
\[ i \hbar \frac{\partial}{\partial t} \Psi (t, x) = H \Psi (t, x), \qquad H = - \frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2} + V (x) \]
を解いて求めたものである。
波束の中心を⭐️で、運動量 \(\hbar k_0\) の古典的な粒子の位置を◉で示してある。
反射後に⭐️が◉より少しだけ遅れるのがわかるだろうか。