Materials
今回はAharonov-Bohm効果について学ぶ。 Aharonov-Bohm効果は、粒子が電場 \( \boldsymbol{E} \) や磁場 (正確には磁束密度) \( \boldsymbol{B} \) のない箇所で運動しているにも関わらず、電磁ポテンシャル \( \boldsymbol{A} \) の影響を受ける効果である。
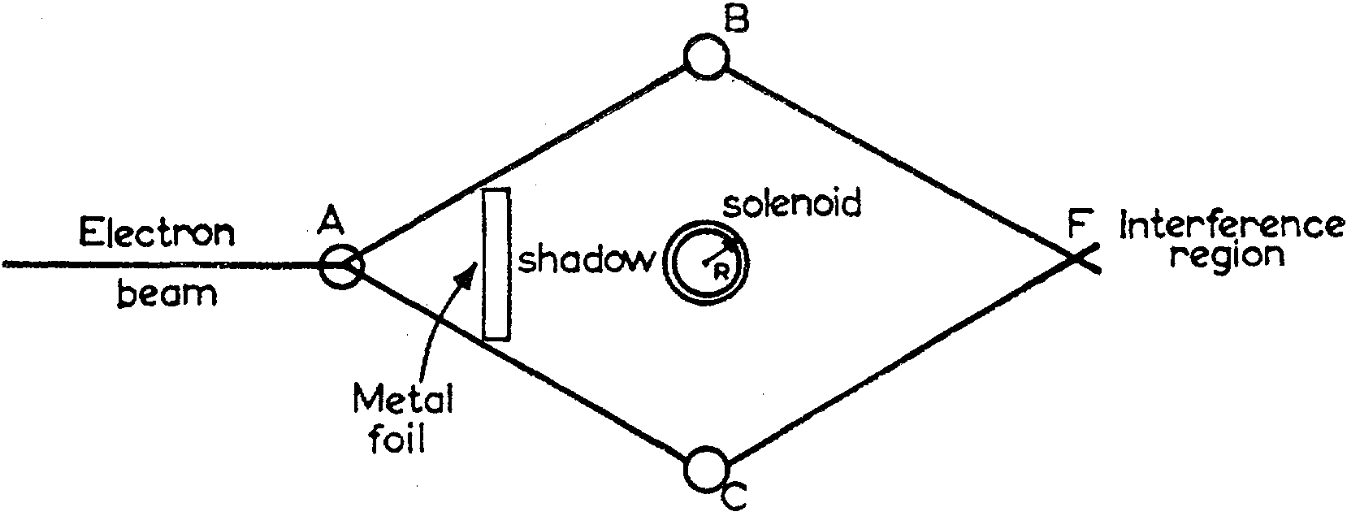
セットアップは以下の図の通りである。 左から入射した電荷 \( q \) の荷電粒子のビームを点Aで2つに分離する。 分離したビームはそれぞれ点B, Cを経由して点Fで干渉を起こす。 2つのビームの間にはソレノイドコイルがあり、一定の磁束 \( \Phi \) が磁束密度 \( \boldsymbol{B} \) で画面手前方向に印加されている。 ソレノイド外部の電磁ポテンシャルは、ソレノイドからの距離を \( r \) として \[ \varphi (t, \boldsymbol{x}) = 0, \] \[ \boldsymbol{A} (t, \boldsymbol{x}) = \frac{\Phi}{2 \pi r} \boldsymbol{e}_\phi, \] である。 粒子のビームが通過する領域では、電場 \( \boldsymbol{E} \) や磁場 (正確には磁束密度) \( \boldsymbol{B} \) はいずれも \( 0 \) である。 この粒子の振る舞いを記述するSchrödinger方程式は、ポテンシャル \( V (t, \boldsymbol{x}) \) の存在下で \[ i \hbar \frac{\partial}{\partial t} \Psi (t, \boldsymbol{x}) = \left[ \frac{1}{2 m} (- i \hbar \boldsymbol{\nabla} - q \boldsymbol{A})^2 + q \varphi (t, \boldsymbol{x}) + V (t, \boldsymbol{x}) \right] \Psi (t, \boldsymbol{x}), \] となる。
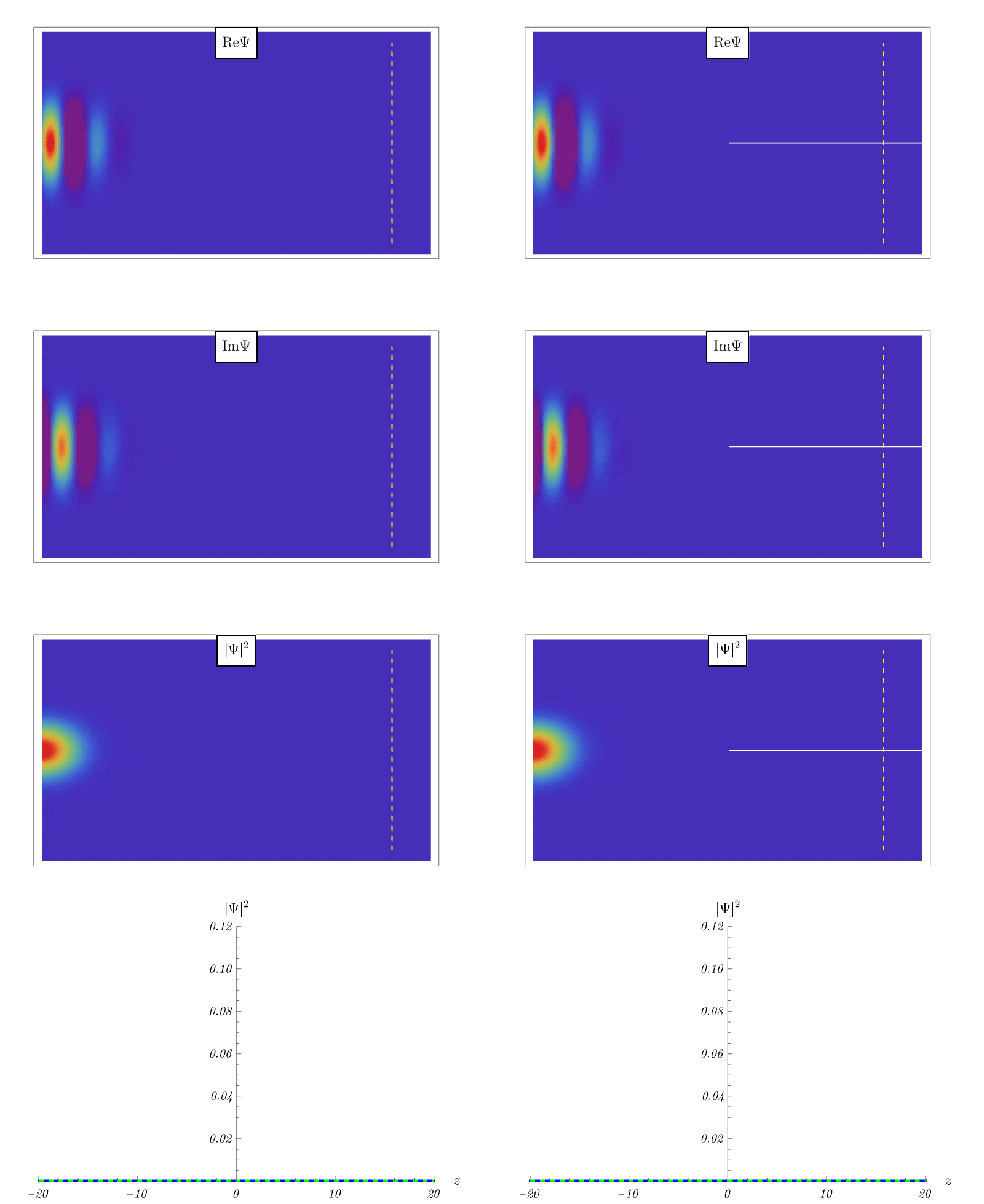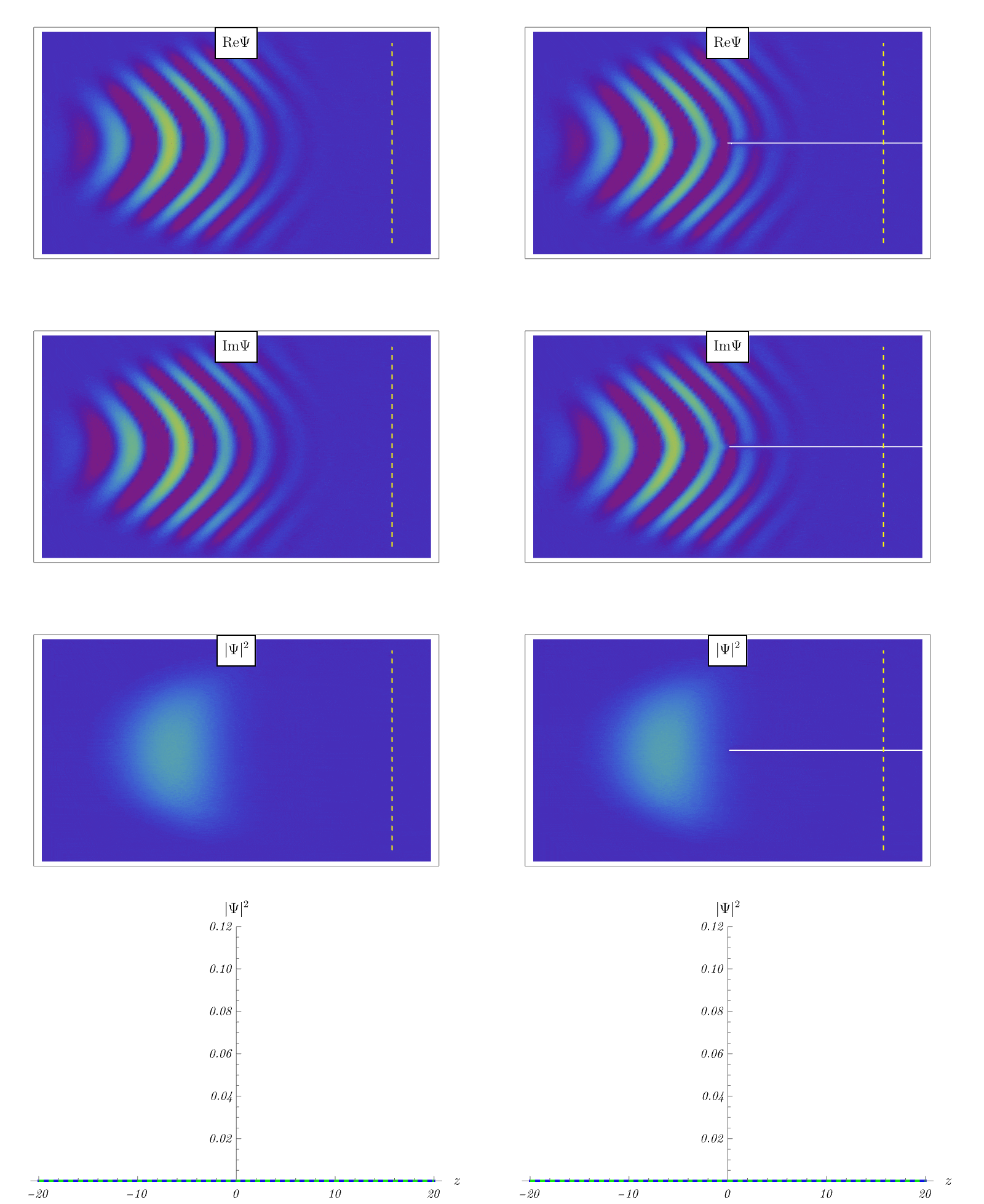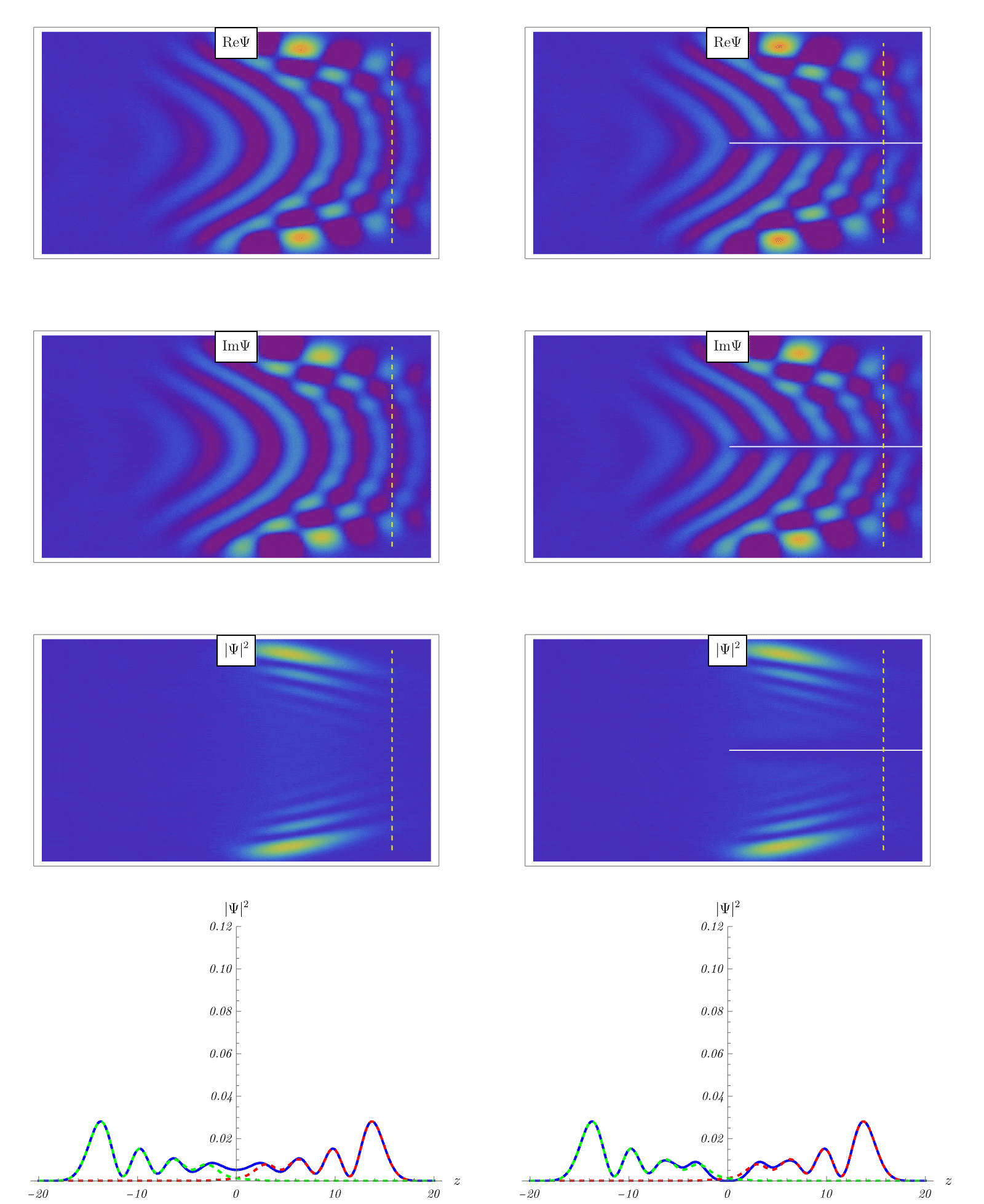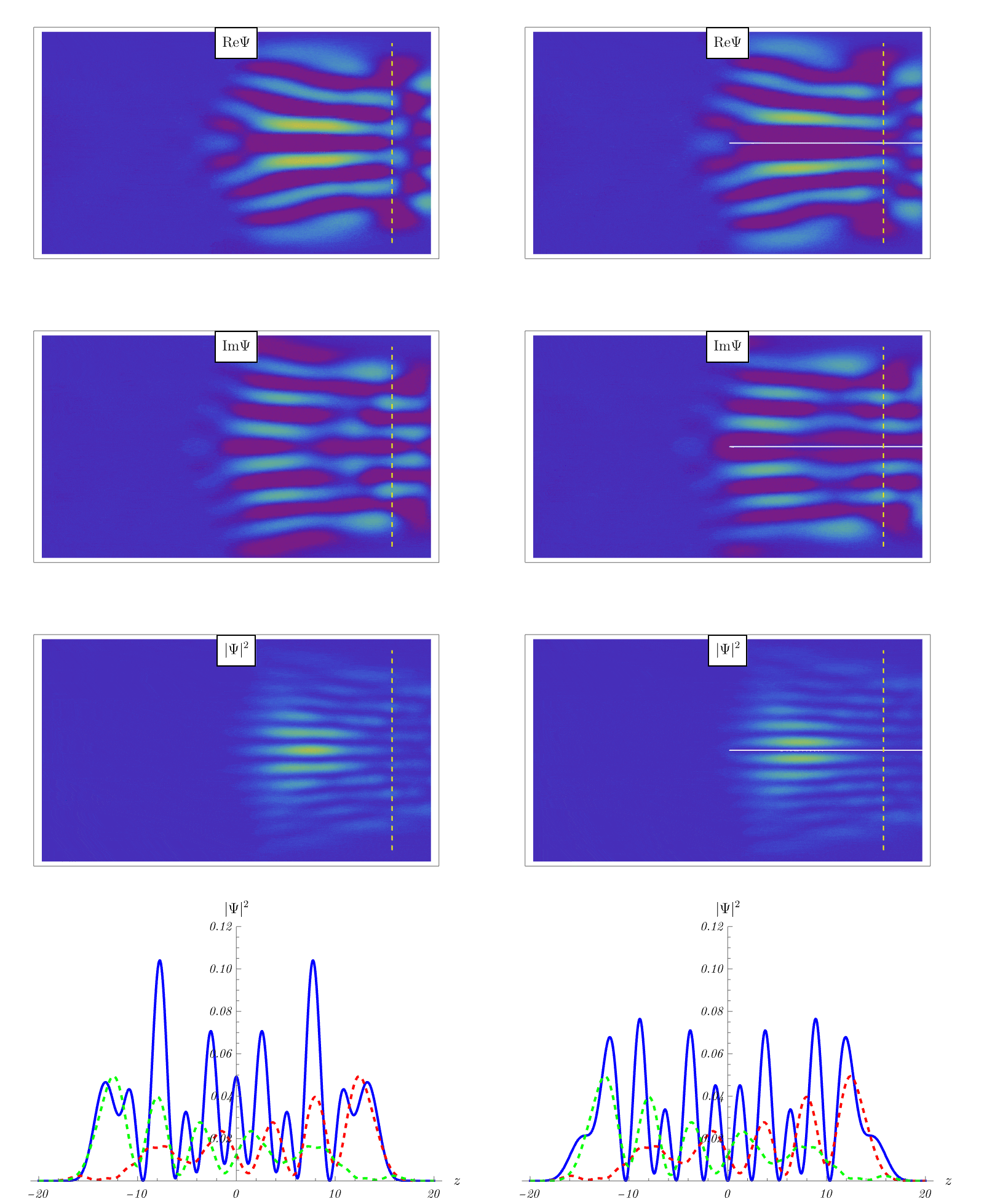
以下のアニメーションでは、原点に上図のソレノイドコイルがあり、粒子のビームを (適当なポテンシャル \( V (t, \boldsymbol{x}) \) により) 2つに分離させ、図の右端付近で再度干渉させている。 左図が磁束 \( \Phi = 0 \) の場合、右図が磁束 \( \Phi > 0 \) の場合である。
黄色の点線上にスクリーンを置き、左右のビームが干渉することにより生じる、粒子の観測確率の干渉縞を考えよう。 スクリーン上の観測確率が最下図に示されている。 原点のソレノイド以外の領域では \( \boldsymbol{E} (t, \boldsymbol{x}) \) も \( \boldsymbol{B} (t, \boldsymbol{x}) \) も \( 0 \) であるにも関わらず、干渉縞のパターンは電磁ポテンシャル \( \boldsymbol{A} (t, \boldsymbol{x}) \) の影響で変化していることがわかる。