Materials
今回は量子論におけるいくつかの重要な現象のうち、Larmor歳差運動とStern-Gerlachの実験について学ぶ。 Larmor歳差運動は前回のアニメーションで見たので、ここではStern-Gerlachの実験を見てみよう。
前回、電荷を持つ粒子にスピンがあると、磁束密度に応じてスピンの向きを変えたがることを見た。 これをもう少し詳細に見よう。 古典電磁気学では、円電流を遠方から見ると、仮想的な磁気双極子が持つ磁気モーメントと区別がつかない。 電荷を持つ粒子のスピンも円電流「みたいなもの」(あくまで類推であることに注意)なので、一般に磁気双極子と同様の磁気モーメント \( \boldsymbol{\mu} \) が生じる。 磁気モーメントは電荷がどのくらい激しくスピンしているかに依存するので、粒子のスピン \( \boldsymbol{S} \) に比例した形で \[ \boldsymbol{\mu} = \gamma \boldsymbol{S}, \] と書く。 実は電気的に中性な粒子でも、それが複合粒子であれば、構成要素間で電荷はキャンセルし合うが磁気モーメントはキャンセルするとは限らないので、一般に磁気モーメントがある。
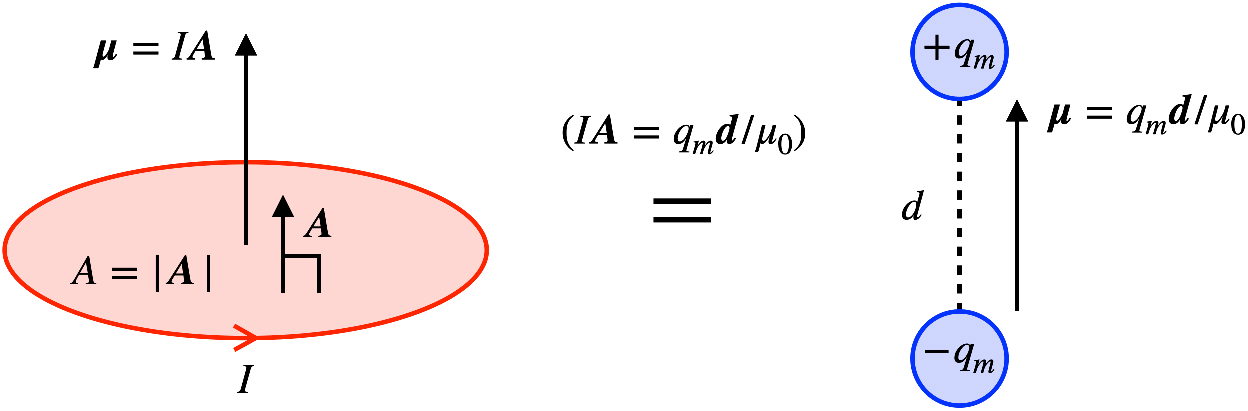
さて、Stern-Gerlachの実験は以下のような実験である。 磁気モーメントを持つ粒子のビームを磁石間に打ち込んでみる。 磁気モーメントは磁気双極子のようなものなので、粒子は磁気モーメント \( \hat{\boldsymbol{\mu}}\) を磁石から生じる磁束密度 \( \boldsymbol{B} \) と揃えたがる。 Hamiltonianで書くと、 \[ \hat{H} = \frac{\hat{\boldsymbol{p}}^2}{2 m} - \hat{\boldsymbol{\mu}} \cdot \boldsymbol{B} = \frac{\hat{\boldsymbol{p}}^2}{2 m} - \gamma \hat{\boldsymbol{S}} \cdot \boldsymbol{B}, \] である。 ちなみにこの最終項 \( - \gamma \hat{\boldsymbol{S}} \cdot \boldsymbol{B} \) が、前回Larmor歳差運動で見た項であった。
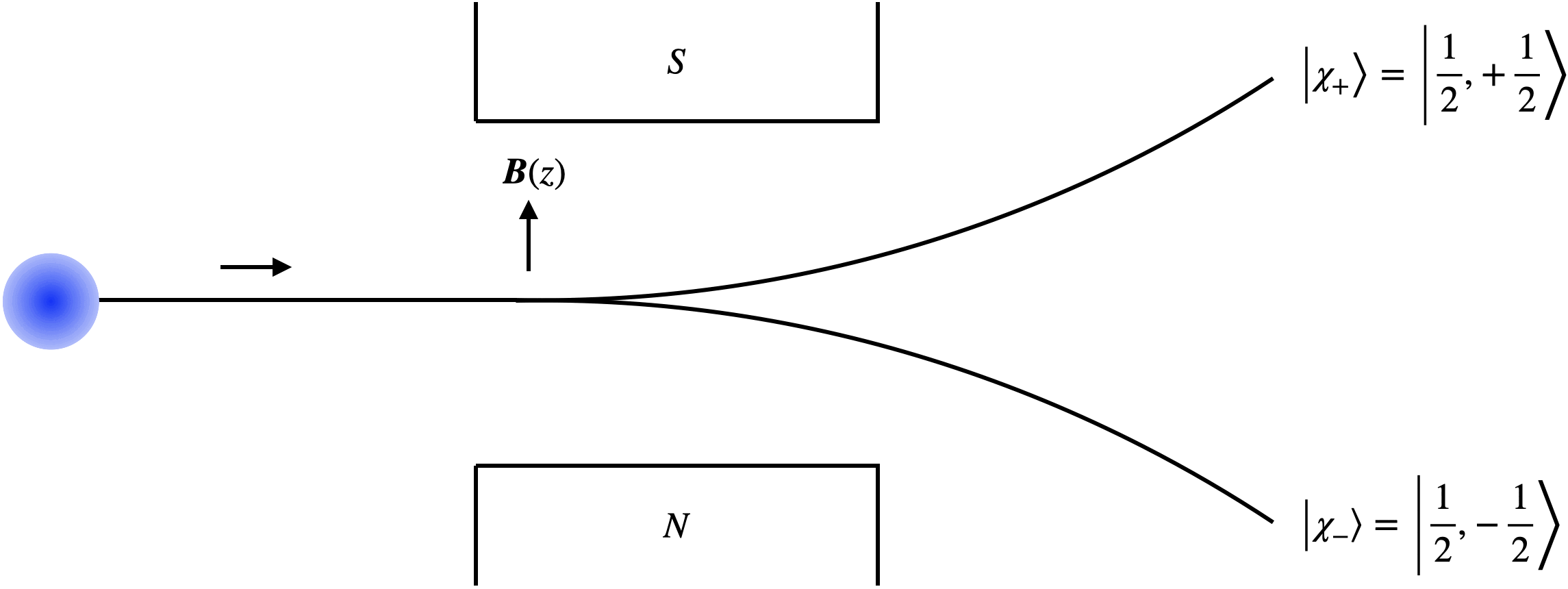
このHamiltonianの下で、粒子はどう振る舞うだろうか。 まず直感的に、Hamiltonianの \( - \gamma \hat{\boldsymbol{S}} \cdot \boldsymbol{B} \) はエネルギー \[ E_+ = - \gamma \frac{\hbar}{2} B_z~\left( \hat{S}_z \, の固有値 \, + \frac{\hbar}{2} \, の状態 \right), \] \[ E_- = + \gamma \frac{\hbar}{2} B_z~\left( \hat{S}_z \, の固有値 \, - \frac{\hbar}{2} \, の状態 \right), \] 分の寄与をするので、\( z \) 方向の磁束密度 \( B_z \) が空間的に変動していると、 \[ F_+ = - \frac{\partial}{\partial z} E_+ = + \gamma \frac{\hbar}{2} \frac{\partial}{\partial z} B_z~\left( \hat{S}_z \, の固有値 \, + \frac{\hbar}{2} \, の状態 \right), \] \[ F_- = - \frac{\partial}{\partial z} E_- = - \gamma \frac{\hbar}{2} \frac{\partial}{\partial z} B_z~\left( \hat{S}_z \, の固有値 \, - \frac{\hbar}{2} \, の状態 \right), \] だけの力が \( z \) 方向に働いて、軌道がずれていくことが予想される。 以下のアニメーションはSchrödinger方程式を解いた結果で、実際、スピンの \( z \) 成分の固有値に応じて軌道が離散的に分離することがわかる。
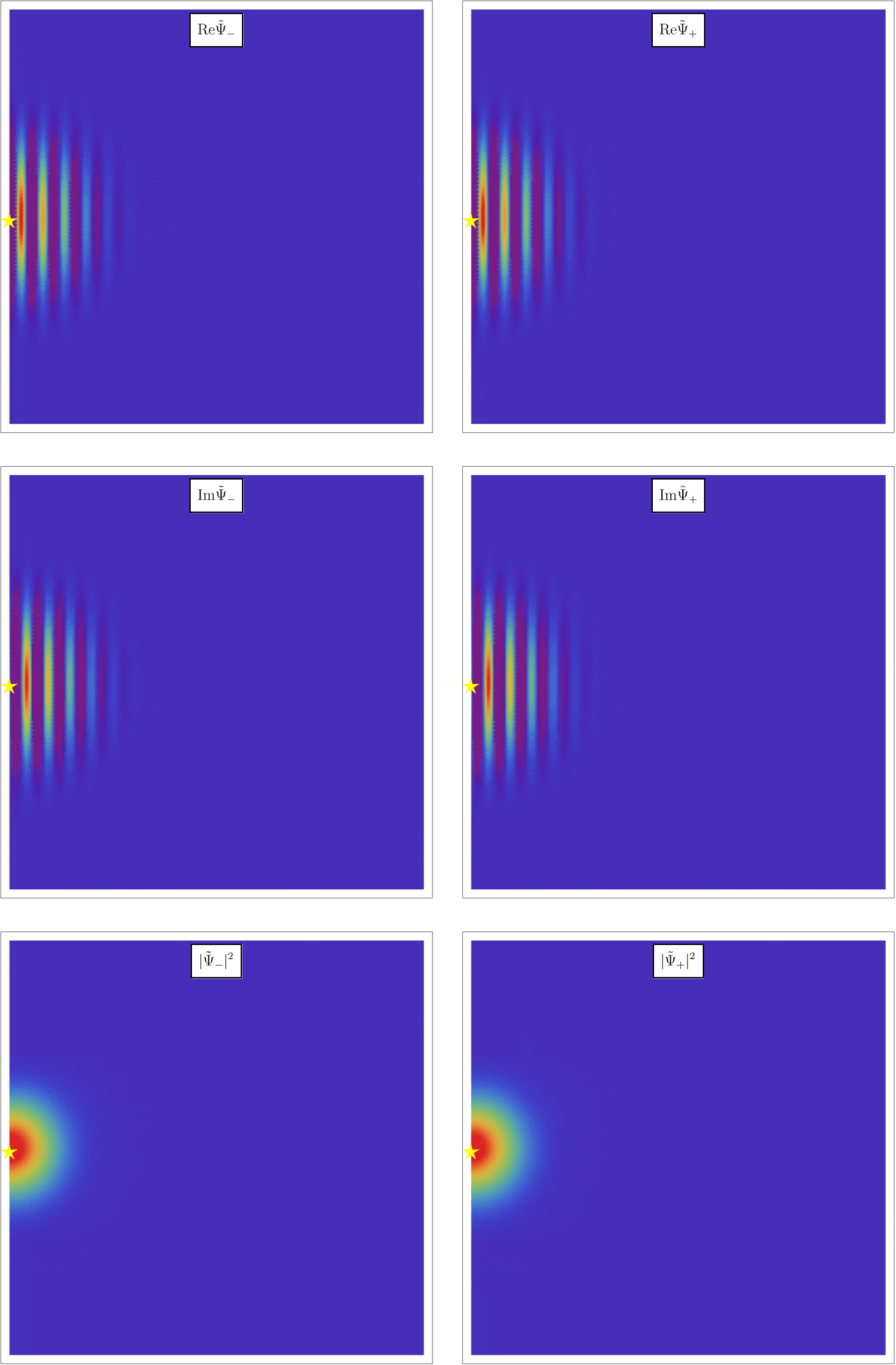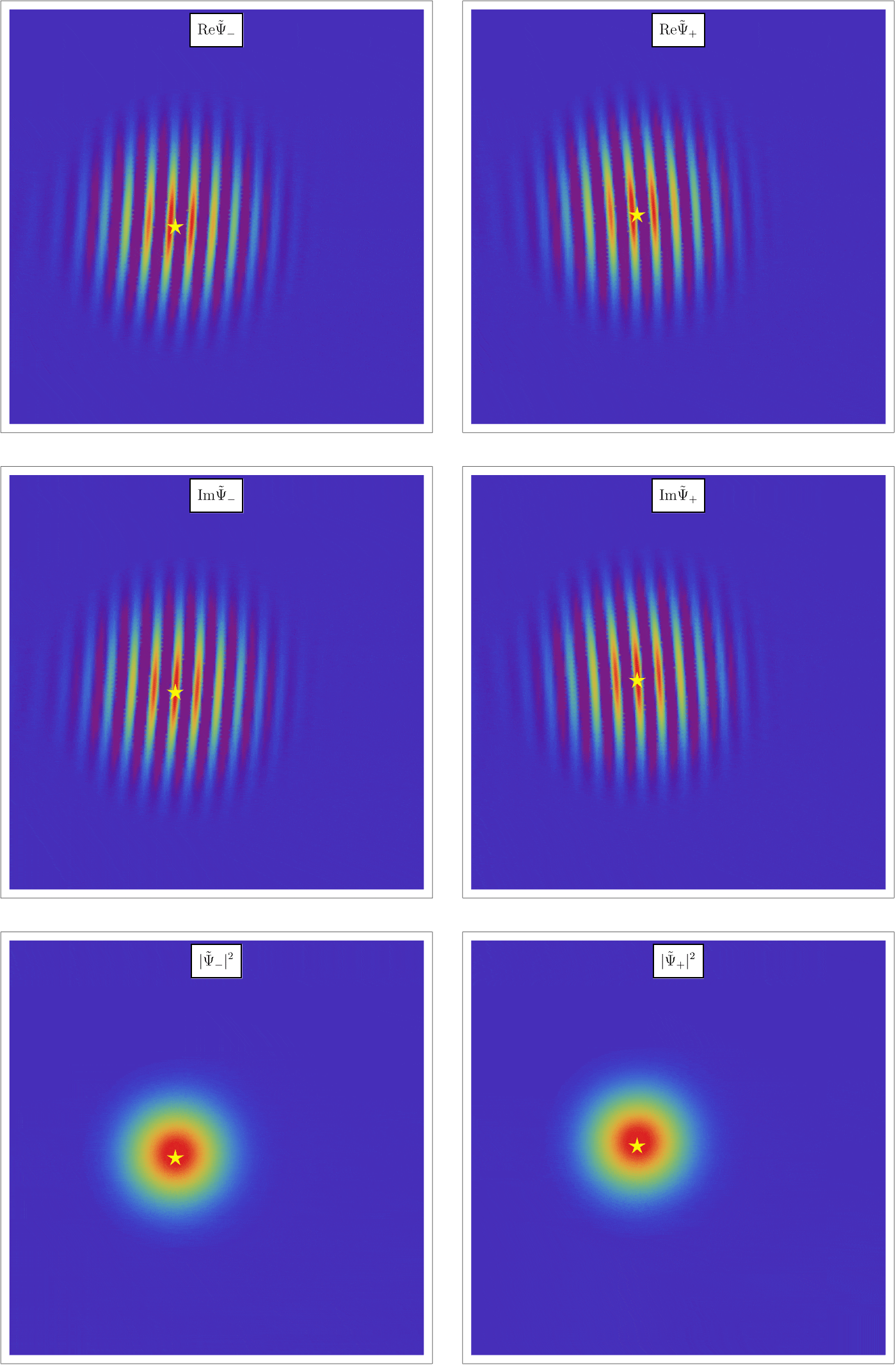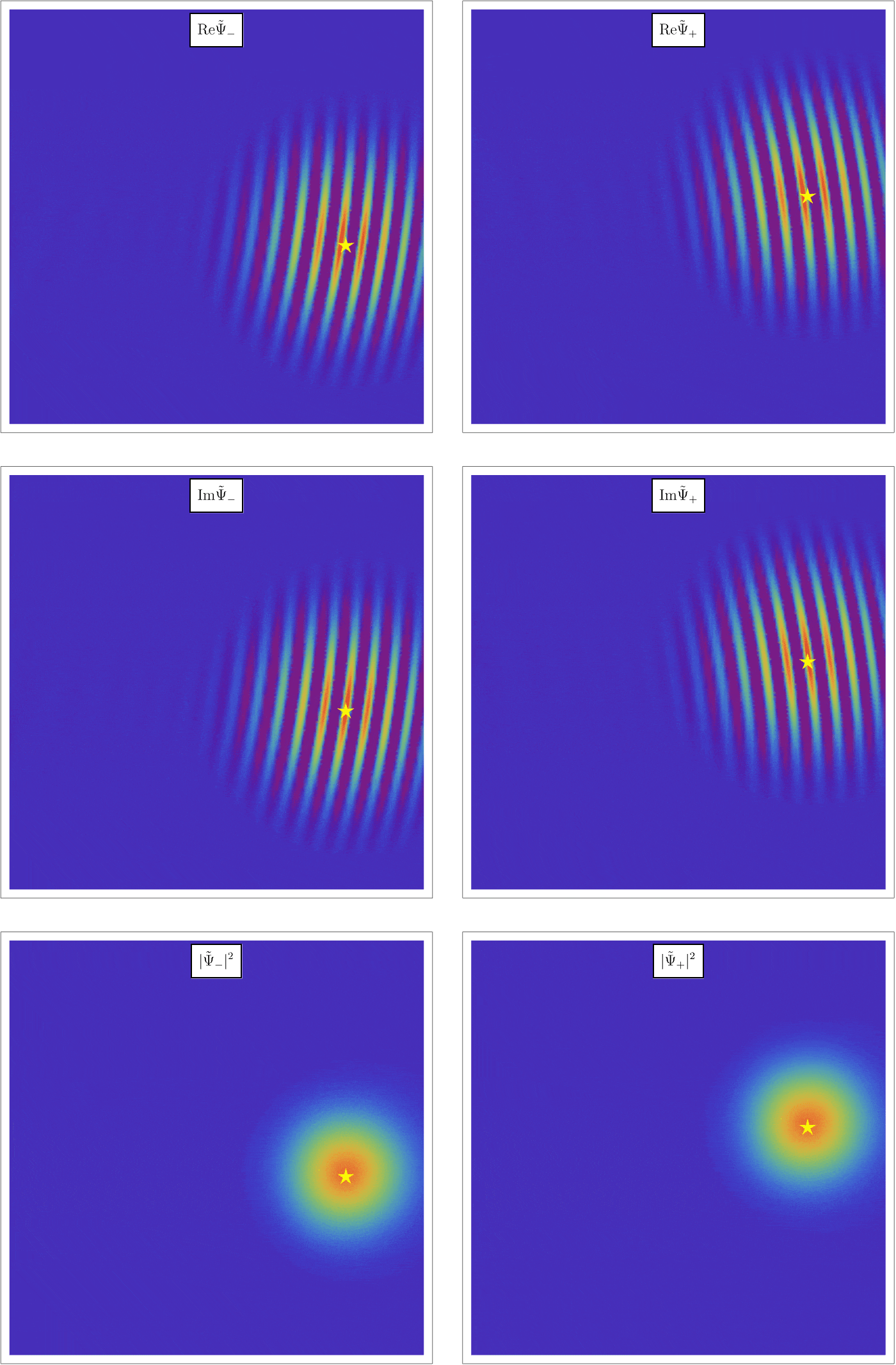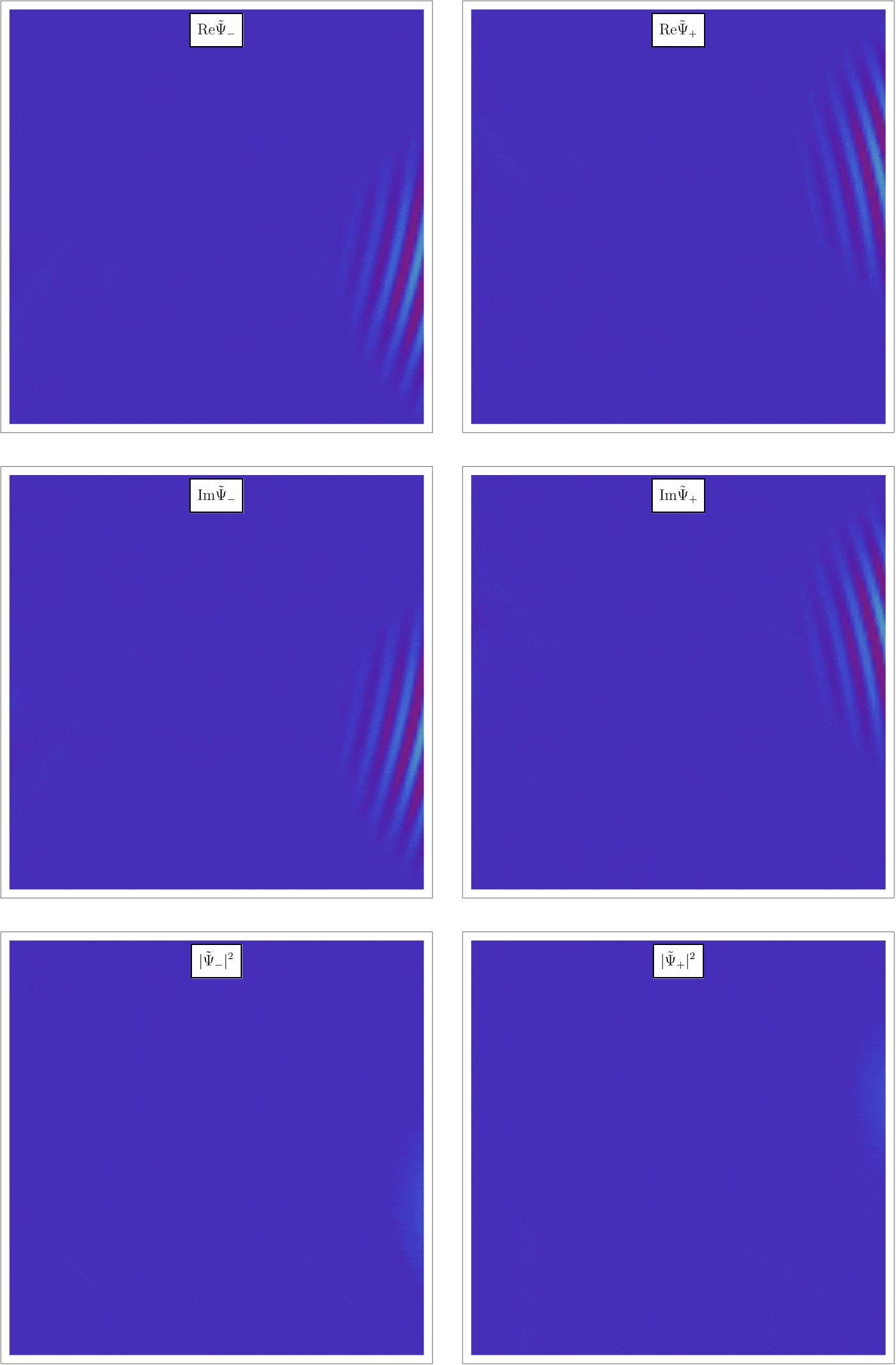
上の直感的な議論をもう少し正確に見よう。 この系は「粒子が時刻 \( t \) に位置 \( \boldsymbol{r} \) にどのくらいの確率で存在するか」だけではなく、「粒子が時刻 \( t \) に位置 \( \boldsymbol{r} \) および \( \hat{S}_z \) の固有値 \( \pm \frac{\hbar}{2} \) にどのくらいの確率で存在するか」で決まっているので、波動関数は \[ \Psi (t, \boldsymbol{r}) = \left( \begin{array}{c} \Psi_+ (t, \boldsymbol{r}) \\\Psi_- (t, \boldsymbol{r}) \end{array} \right), \] となる。 Schrödinger方程式を書いてみると \[ i \hbar \frac{\partial}{\partial t} \Psi (t, \boldsymbol{r}) = - \frac{\hbar^2}{2 m} \nabla^2 \Psi (t, \boldsymbol{r}) - \gamma (\hat{S}_x B_x + \hat{S}_y B_y + \hat{S}_z B_z) \Psi (t, \boldsymbol{r}), \] であり、ここに \( z \) 方向の一定磁場 \( B_0 \) とその周りの小さな揺らぎ \[ B_x = - \alpha x, \qquad B_y = 0, \qquad B_z = B_0 + \alpha z, \] を代入してみる。 \( x \) 方向にも磁場があるのは、Maxwell方程式の \( \nabla \cdot \boldsymbol{B} = 0 \) を満たすためである。 すると2つの方程式 \[ i \hbar \frac{\partial}{\partial t} \Psi_+ (t, \boldsymbol{r}) = - \frac{\hbar^2}{2 m} \nabla^2 \Psi_+ (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma \alpha x \Psi_- (t, \boldsymbol{r}) - \frac{\hbar}{2} \gamma (B_0 + \alpha z) \Psi_+ (t, \boldsymbol{r}) , \] \[ i \hbar \frac{\partial}{\partial t} \Psi_- (t, \boldsymbol{r}) = - \frac{\hbar^2}{2 m} \nabla^2 \Psi_- (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma \alpha x \Psi_+ (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma (B_0 + \alpha z) \Psi_- (t, \boldsymbol{r}) , \] が得られる。 この方程式では \( \Psi_+ (t, \boldsymbol{r}) \) と \( \Psi_- (t, \boldsymbol{r}) \) が絡み合っているが、実は \( B_0 \) が大きい極限で実質的に \( x \) に比例する項は無視できて、 \[ i \hbar \frac{\partial}{\partial t} \Psi_+ (t, \boldsymbol{r}) \simeq - \frac{\hbar^2}{2 m} \nabla^2 \Psi_+ (t, \boldsymbol{r}) - \frac{\hbar}{2} \gamma (B_0 + \alpha z) \Psi_+ (t, \boldsymbol{r}) , \] \[ i \hbar \frac{\partial}{\partial t} \Psi_- (t, \boldsymbol{r}) \simeq - \frac{\hbar^2}{2 m} \nabla^2 \Psi_- (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma (B_0 + \alpha z) \Psi_- (t, \boldsymbol{r}) , \] が得られる。 実際、\( \Psi_\pm (t, \boldsymbol{r}) =: e^{\pm \frac{i \gamma B_0 t}{2}} \tilde{\Psi}_\pm (t, \boldsymbol{r}) \) とすると \[ i \hbar \frac{\partial}{\partial t} \tilde{\Psi}_+ (t, \boldsymbol{r}) = - \frac{\hbar^2}{2 m} \nabla^2 \tilde{\Psi}_+ (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma \alpha x e^{- i \gamma \alpha B_0} \tilde{\Psi}_- (t, \boldsymbol{r}) - \frac{\hbar}{2} \gamma \alpha z \tilde{\Psi}_+ (t, \boldsymbol{r}) , \] \[ i \hbar \frac{\partial}{\partial t} \tilde{\Psi}_- (t, \boldsymbol{r}) = - \frac{\hbar^2}{2 m} \nabla^2 \tilde{\Psi}_- (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma \alpha x e^{i \gamma \alpha B_0} \tilde{\Psi}_+ (t, \boldsymbol{r}) + \frac{\hbar}{2} \gamma \alpha z \tilde{\Psi}_- (t, \boldsymbol{r}) , \] となるが、\( x \) 比例項は激しく振動するため無視できる。 上のアニメーションではこれを適切な初期条件 \[ \tilde{\Psi}_+ (t = 0, \boldsymbol{r}) = \tilde{\Psi}_- (t = 0, \boldsymbol{r}) \propto e^{i p_0 x} e^{- \frac{x^2 + z^2}{2 \sigma^2}}, \] で解いている。