Materials
今回は角運動量 \( \hat{\textbf{L}} = \hat{\textbf{r}} \times \hat{\textbf{p}} \) の交換関係 \[ [\hat{L}_x, \hat{L}_y] = i \hbar \hat{L}_z, \qquad [\hat{L}_y, \hat{L}_z] = i \hbar \hat{L}_x, \qquad [\hat{L}_z, \hat{L}_x] = i \hbar \hat{L}_y, \] について学ぶ。 まずは、運動量 \( \hat{\textbf{p}} \) が系に微小推進を引き起こし、角運動量 \( \hat{\textbf{L}} \) が系に微小回転を引き起こす様子を見る。 その後、角運動量の交換関係を見る。
11-1. 並進
まずは1次元Schrödinger方程式に戻って、並進の復習をする。 任意の状態 \( \ket{\psi} \) に対し運動量演算子 \( \hat{p} \) が作用すると、\( \ket{x} \) 表示で見たときに、微分演算子 \[ \bra{x} \hat{p} \ket{\psi} = - i \hbar \frac{d}{d x} \braket{x | \psi}, \] になっていることを学んだ。 この運動量演算子を指数の肩に乗せた \( e^{- \frac{i a \hat{p}}{\hbar}} \) は、波動関数を空間方向に \( a \) だけ進ませる効果がある \[ \bra{x} e^{- \frac{i a \hat{p}}{\hbar}} \ket{\psi} = e^{- a \frac{d}{dx}} \braket{x | \psi} = \braket{x - a | \psi}. \] つまり、任意の関数 \( f(x) \) に対し、微分が肩に乗った \( e^{- a \frac{d}{dx}} \) を演算すると、 \( a \) だけ進んだ \( f(x - a) \) になると言っている。 \[ e^{- a \frac{d}{dx}} f (x) = f (x - a). \] 本当だろうか。 確かめてみよう。 以下のアニメーションでは、 \[ e^{- a \frac{d}{dx}} = \lim_{N \to \infty} \left(1 - \frac{a}{N} \frac{d}{dx} \right)^N, \] であることに注目し、適当な関数 \( f (x) \) に演算 \( \left(1 - \frac{a}{N} \frac{d}{dx} \right) \) を \( N \) 回作用させた結果を、\( N = 1, 2, \cdots \) に対して表示している。 このアニメーションでは並進距離を \( a = 1 \) としている。 初めの \( N = 1, 2 \) では元の関数形とは関数形になるが、\( N \) を増やしたときの収束先は、確かに元の関数形を横にずらした形になっている。
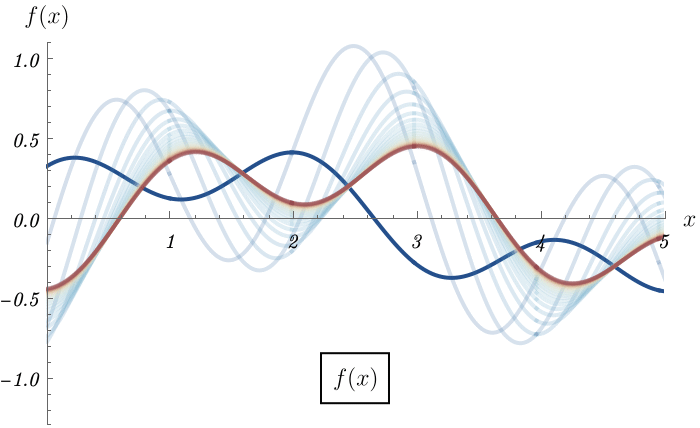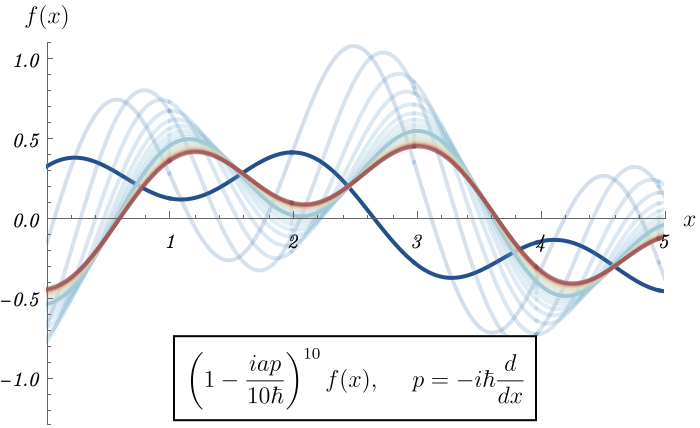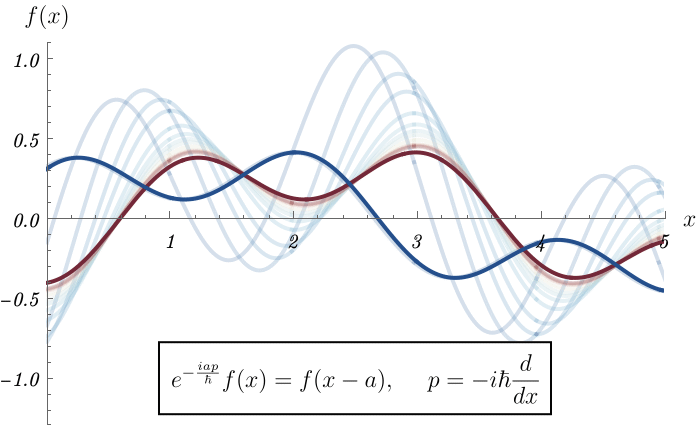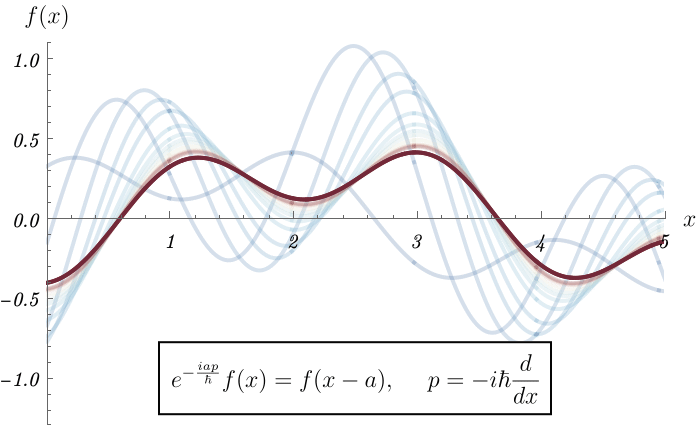
これは数学的には実は簡単で、指数を展開したものが \( f (x - a) \) のTaylor展開になっていることから理解できる。 \[ e^{- a \frac{d}{dx}} f (x) = \sum_{n = 0}^\infty \frac{(- a)^n}{n!} \left( \frac{d}{dx} \right)^n f (x) = f (x - a). \]
11-2. 回転
さて、本題の角運動量に進もう。 任意の状態 \( \ket{\psi} \) に対し角運動量演算子 \( \hat{L} \) が作用すると、球座標表示 \( \ket{r, \theta, \phi} \) で見たときに、 \[ \bra{r, \theta, \phi} \hat{L}_x \ket{\psi} = - i \hbar \left( - \sin \theta \frac{\partial}{\partial\theta} - \frac{\cos \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \braket{r, \theta, \phi | \psi}, \] \[ \bra{r, \theta, \phi} \hat{L}_y \ket{\psi} = - i \hbar \left( \cos \theta \frac{\partial}{\partial\theta} - \frac{\sin \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \braket{r, \theta, \phi | \psi}, \] \[ \bra{r, \theta, \phi} \hat{L}_z \ket{\psi} = - i \hbar \frac{\partial}{\partial\phi} \braket{r, \theta, \phi | \psi}, \] になっていることを講義で学ぶ。 運動量の場合と同じく、これら角運動量演算子を指数の肩に乗せた \( e^{- \frac{i \theta_x \hat{L}_x}{\hbar}},~e^{- \frac{i \theta_y \hat{L}_y}{\hbar}},~e^{- \frac{i \theta_z \hat{L}_z}{\hbar}} \) は、波動関数を \( x, y, z \) 軸周りにそれぞれ \( \theta_x, \theta_y, \theta_z \) だけ回転させる効果がある。 つまり、任意の関数 \( f (\theta, \phi) \) に対し、 \[ \exp \left[ - \theta_x \left( - \sin \theta \frac{\partial}{\partial\theta} - \frac{\cos \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right] f (\theta, \phi), \] \[ \exp \left[ - \theta_x \left( \cos \theta \frac{\partial}{\partial\theta} - \frac{\sin \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right] f (\theta, \phi), \] \[ \exp \left[ - \theta_z \frac{\partial}{\partial\phi} \right] f (\theta, \phi), \] は、波動関数を \( x, y, z \) 軸周りに \( \theta_x, \theta_y, \theta_z \) だけ回転させる効果がある。 \( z \) 軸周りの回転は単に \( \phi \) 微分であり、運動量の場合と本質的に同じなので、\( x, y\) 軸周りの回転だけ見てみよう。 以下のアニメーションでは、並進の場合と同じく \[ \exp \left[ - \theta_x \left( - \sin \theta \frac{\partial}{\partial\theta} - \frac{\cos \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right] = \lim_{N \to \infty} \left[ 1 - \frac{\theta_x}{N} \left( - \sin \theta \frac{\partial}{\partial\theta} - \frac{\cos \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right]^N, \] \[ \exp \left[ - \theta_y \left( \cos \theta \frac{\partial}{\partial\theta} - \frac{\sin \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right] = \lim_{N \to \infty} \left[ 1 - \frac{\theta_y}{N} \left( \cos \theta \frac{\partial}{\partial\theta} - \frac{\sin \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right]^N, \] であることに注目し、適当な関数 \( f (\theta, \phi) \) に演算 \( \left[ 1 - \frac{\theta_x}{N} \left( - \sin \theta \frac{\partial}{\partial\theta} - \frac{\cos \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right] \) および \( \left[ 1 - \frac{\theta_y}{N} \left( \cos \theta \frac{\partial}{\partial\theta} - \frac{\sin \phi}{\tan \theta} \frac{\partial}{\partial\phi} \right) \right] \) をそれぞれ \( N \) 回作用させた結果を、\( N = 1, 2, \cdots \) に対して表示している。 このアニメーションでは \( \theta_x = \theta_y = \frac{\pi}{2} \) としている。 \( N \) を増やしたときの収束先は、確かに元の関数形を回転したものになっている。
11-3. 角運動量の交換関係
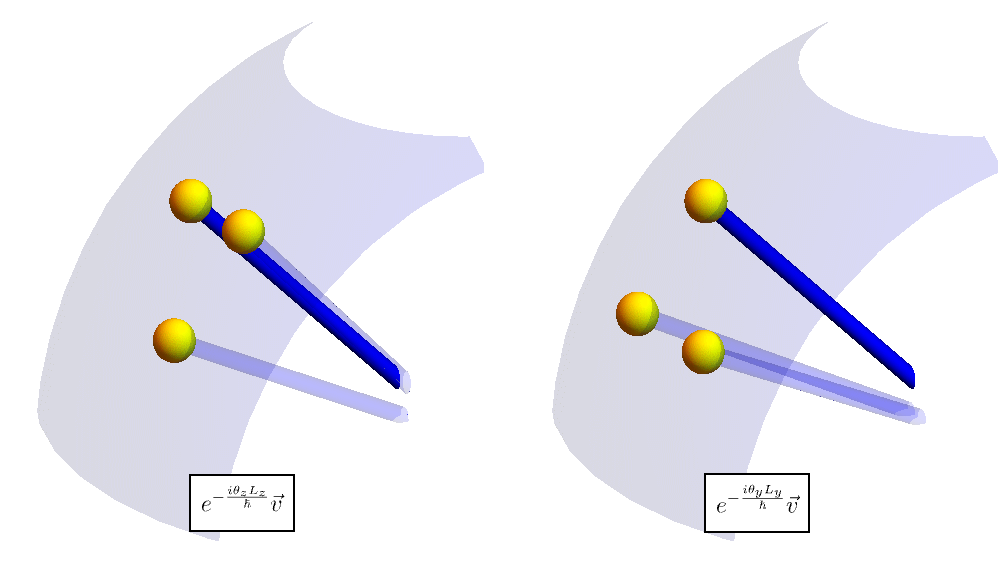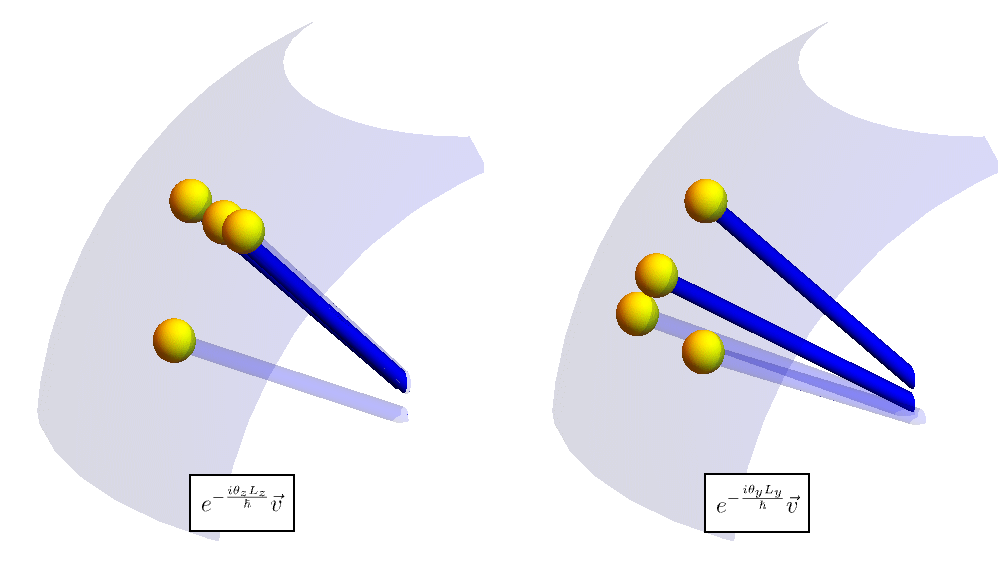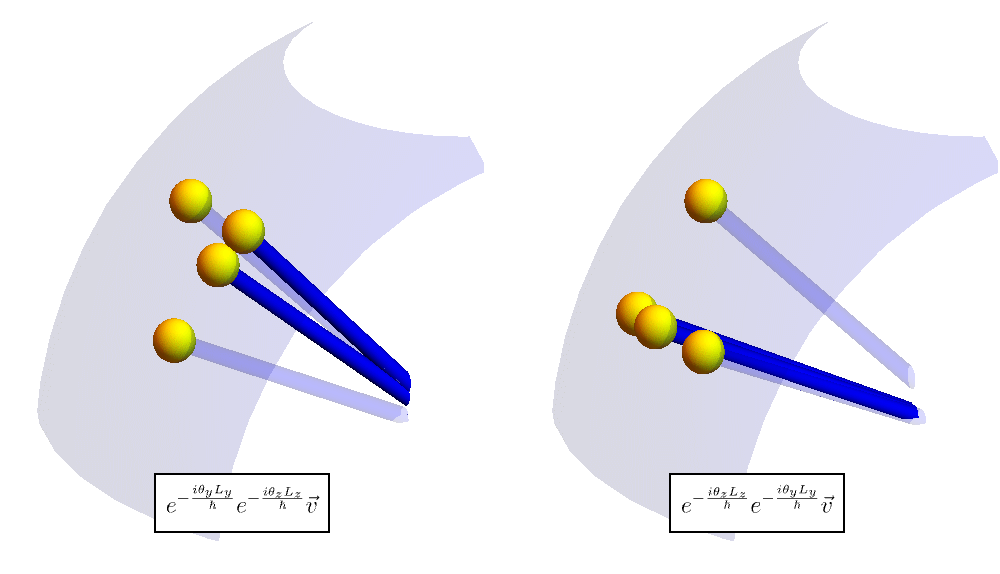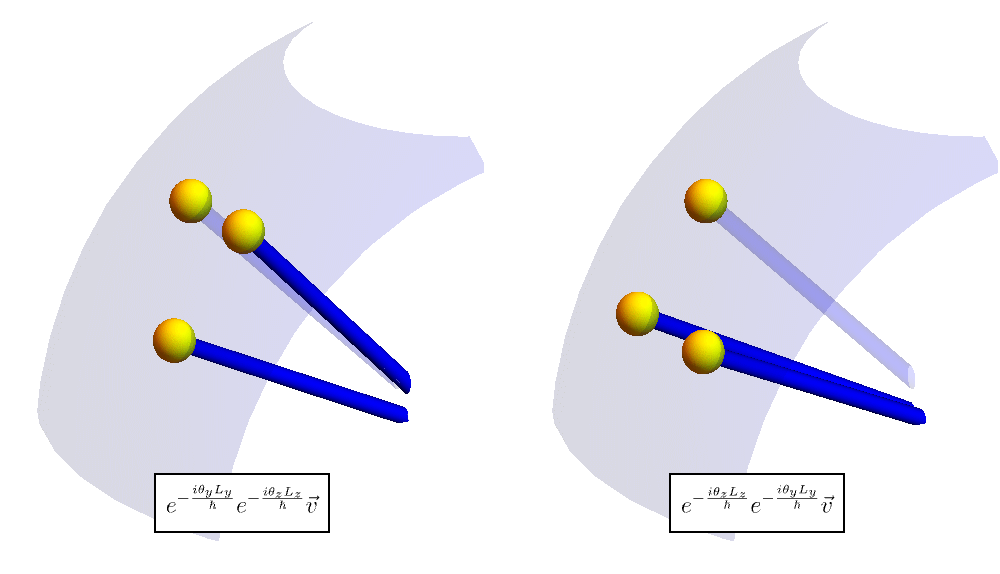
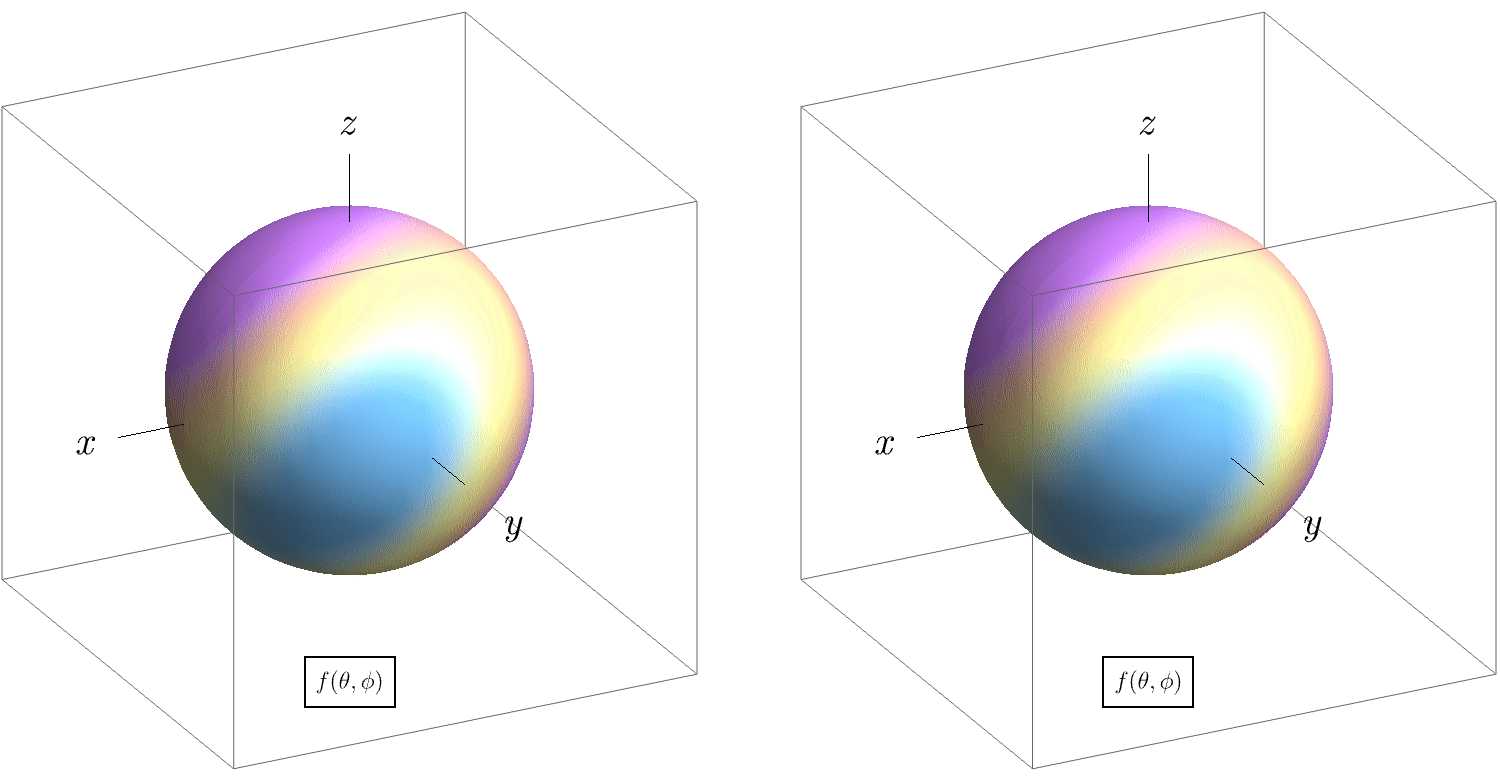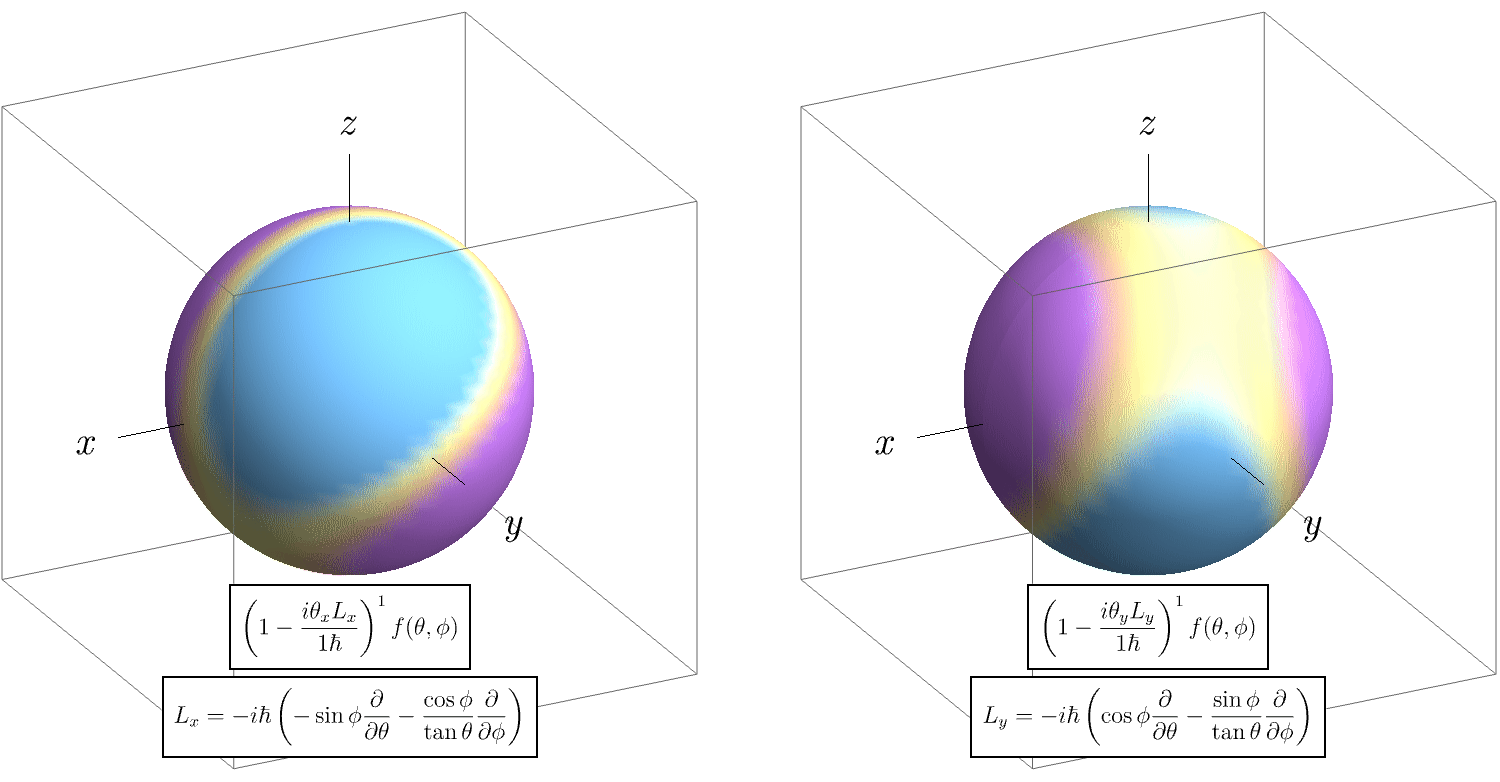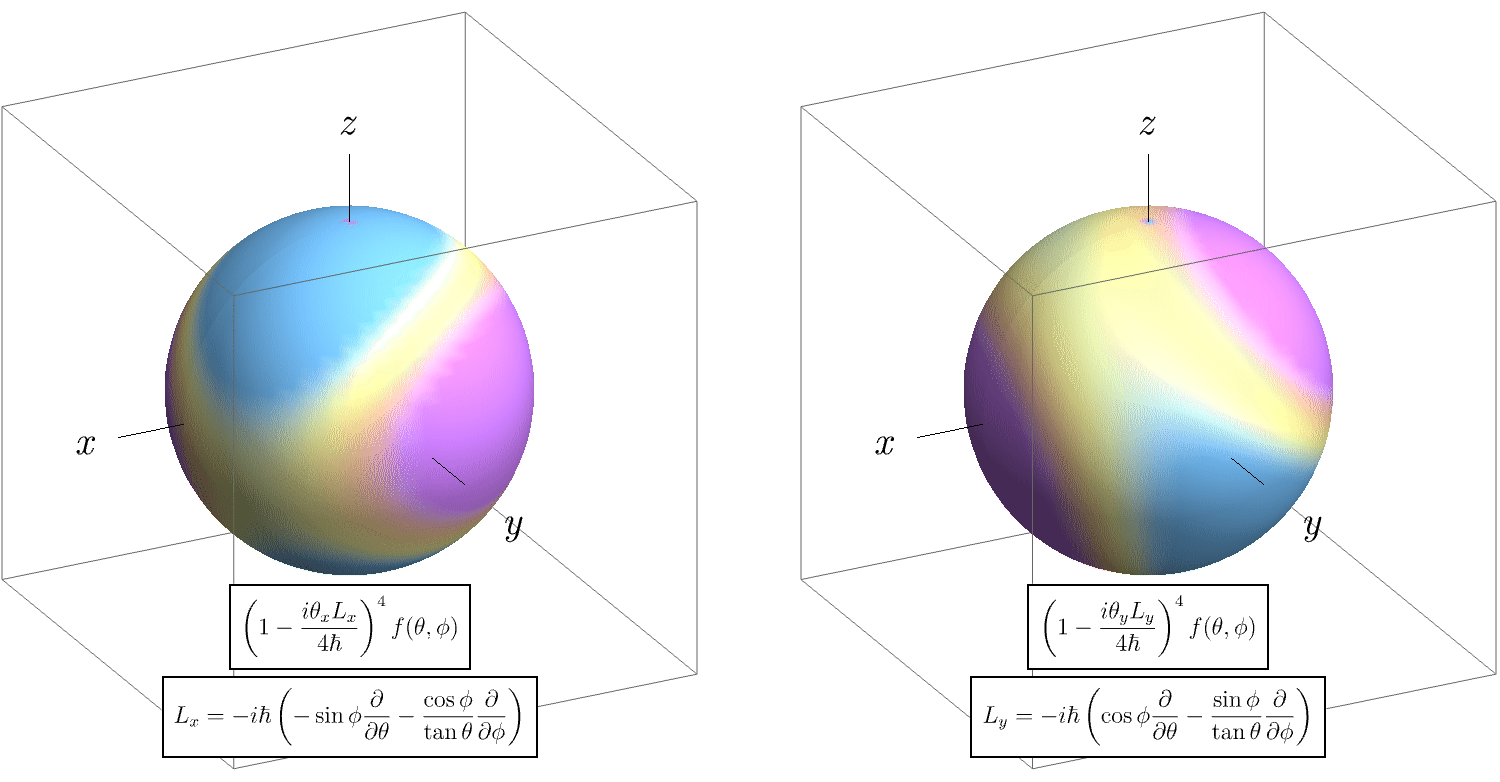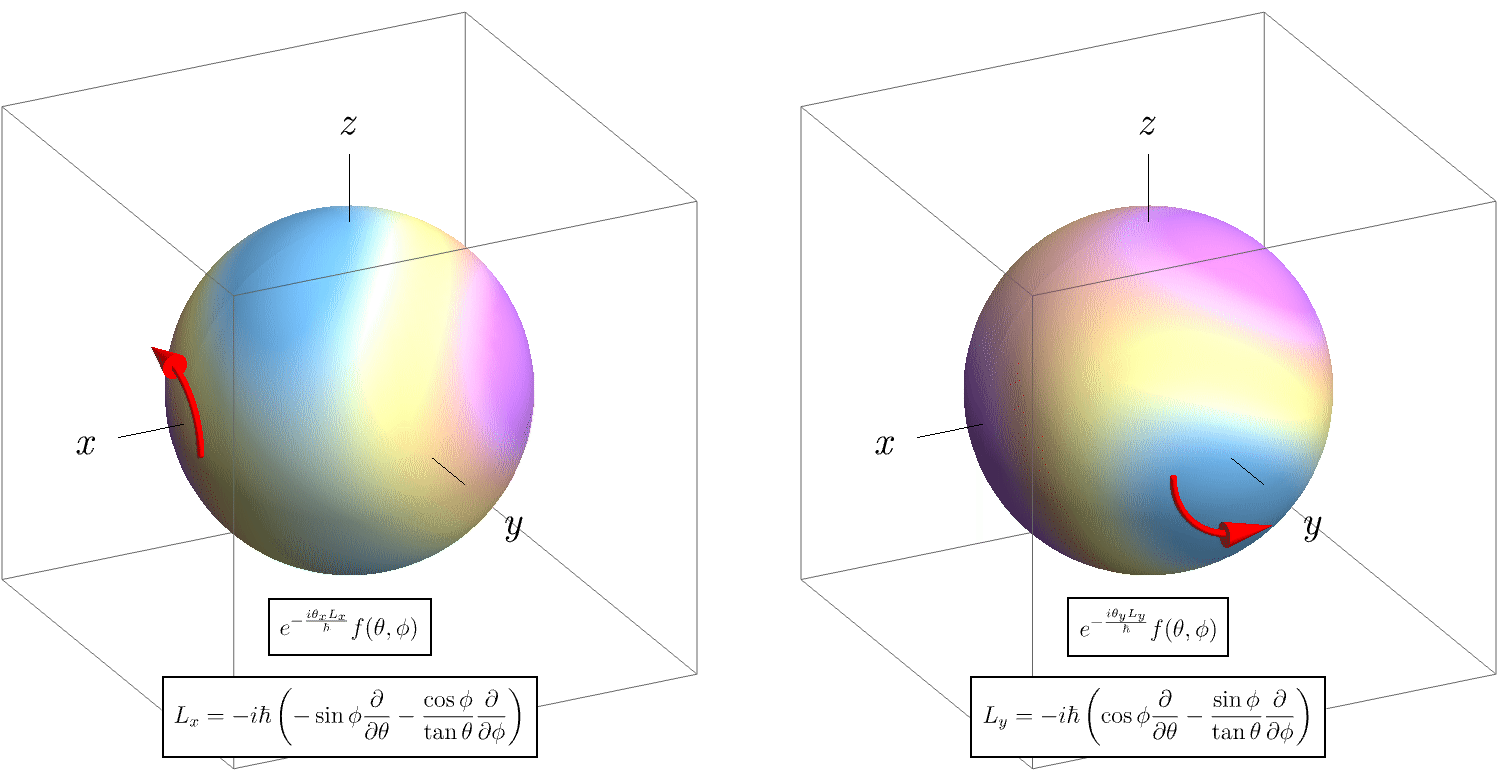
さて、角運動量 \( \hat{\textbf{L}} = \hat{\textbf{r}} \times \hat{\textbf{p}} \) の交換関係 \[ [\hat{L}_x, \hat{L}_y] = i \hbar \hat{L}_z, \qquad [\hat{L}_y, \hat{L}_z] = i \hbar \hat{L}_x, \qquad [\hat{L}_z, \hat{L}_x] = i \hbar \hat{L}_y, \] は何を意味しているのだろうか。 以下のアニメーションは、先程のような関数の代わりに、(見やすさを考慮して)ベクトルを回転させた様子を表している。 左図では「\( z \) 軸周り \( \to \) \( y \) 軸周り」の順に、右図では「\( y \) 軸周り \( \to \) \( z \) 軸周り」の順に回転させている。 回転の順番が異なると、最終的な矢印の位置が異なることがわかる。

なぜ回転の順番で結果に差が出るのか。 上図では \( y \) 軸周りと \( z \) 軸周りに大きな回転をしているが、大きな回転をしたときに差が出る原因は、突き詰めれば小さな回転にあるに違いない。 そこで小さな回転を見てみよう。 両者の差は \[ e^{- \frac{i \theta_y \hat{L}_y}{\hbar}} e^{- \frac{i \theta_z \hat{L}_z}{\hbar}} \, \vec{v} - e^{- \frac{i \theta_z \hat{L}_z}{\hbar}} e^{- \frac{i \theta_y \hat{L}_y}{\hbar}} \, \vec{v} \simeq \left( 1 - \frac{i \theta_y \hat{L}_y}{\hbar} \right) \left( 1 - \frac{i \theta_z \hat{L}_z}{\hbar} \right) \vec{v} - \left( 1 - \frac{i \theta_z \hat{L}_z}{\hbar} \right) \left( 1 - \frac{i \theta_y \hat{L}_y}{\hbar} \right) \vec{v} \simeq - \frac{\theta_y \theta_z}{\hbar^2} [\hat{L}_y, \hat{L}_z] \, \vec{v}, \] となる。\( [\hat{L}_y, \hat{L}_z] = i \hbar \hat{L}_x \) なので \[ - \frac{\theta_y \theta_z}{\hbar^2} [\hat{L}_y, \hat{L}_z] \, \vec{v} = - \frac{i \theta_y \theta_z}{\hbar} \hat{L}_x \, \vec{v} \simeq e^{- i \theta_y \theta_z \hat{L}_x} \, \vec{v} - \vec{v}, \] となる。 つまり、「\( z \) 軸周りに角度 \( \theta_z \) 回転 \( \to \) \( y \) 軸周りに角度 \( \theta_y \) 回転」と「\( y \) 軸周りに角度 \( \theta_y \) 回転 \( \to \) \( z \) 軸周りに角度 \( \theta_z \) 回転」の差は「\( x \) 軸周りに角度 \( \theta_y \theta_z \) 回転」と言っている。 本当だろうか? 以下のアニメーションは微小な \( \theta_y \) および \( \theta_z \) だけ \( \vec{v} \) を回した例である。 よく見ると、最終的なボールの位置が少しだけ異なることがわかる。 交換関係 \[ [\hat{L}_y, \hat{L}_z] = i \hbar \hat{L}_x, \] は、左図の最終位置から右図の最終位置に持っていくには、ほんの少しだけ \( x \) 軸周りに回す必要があることを意味している。