Materials
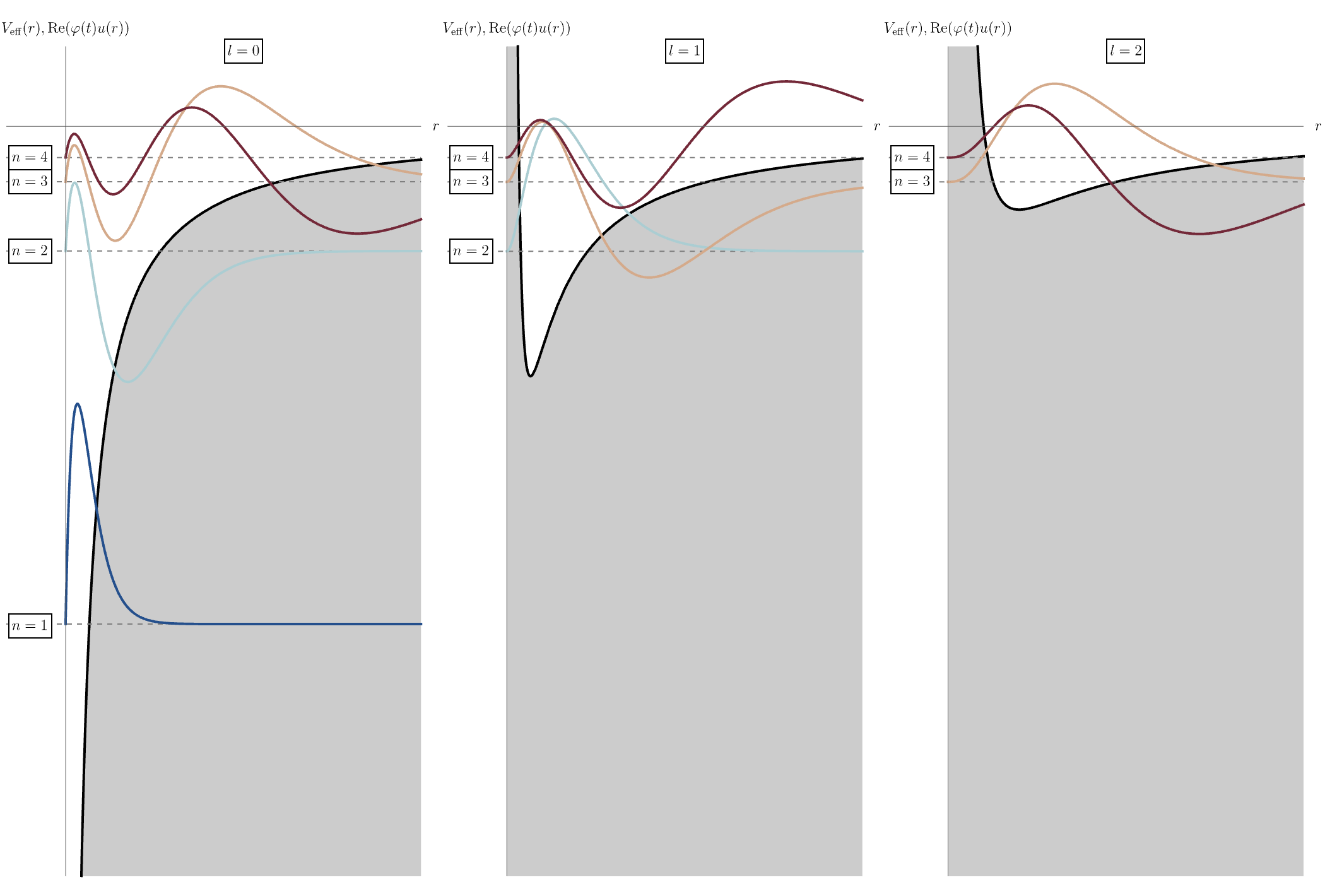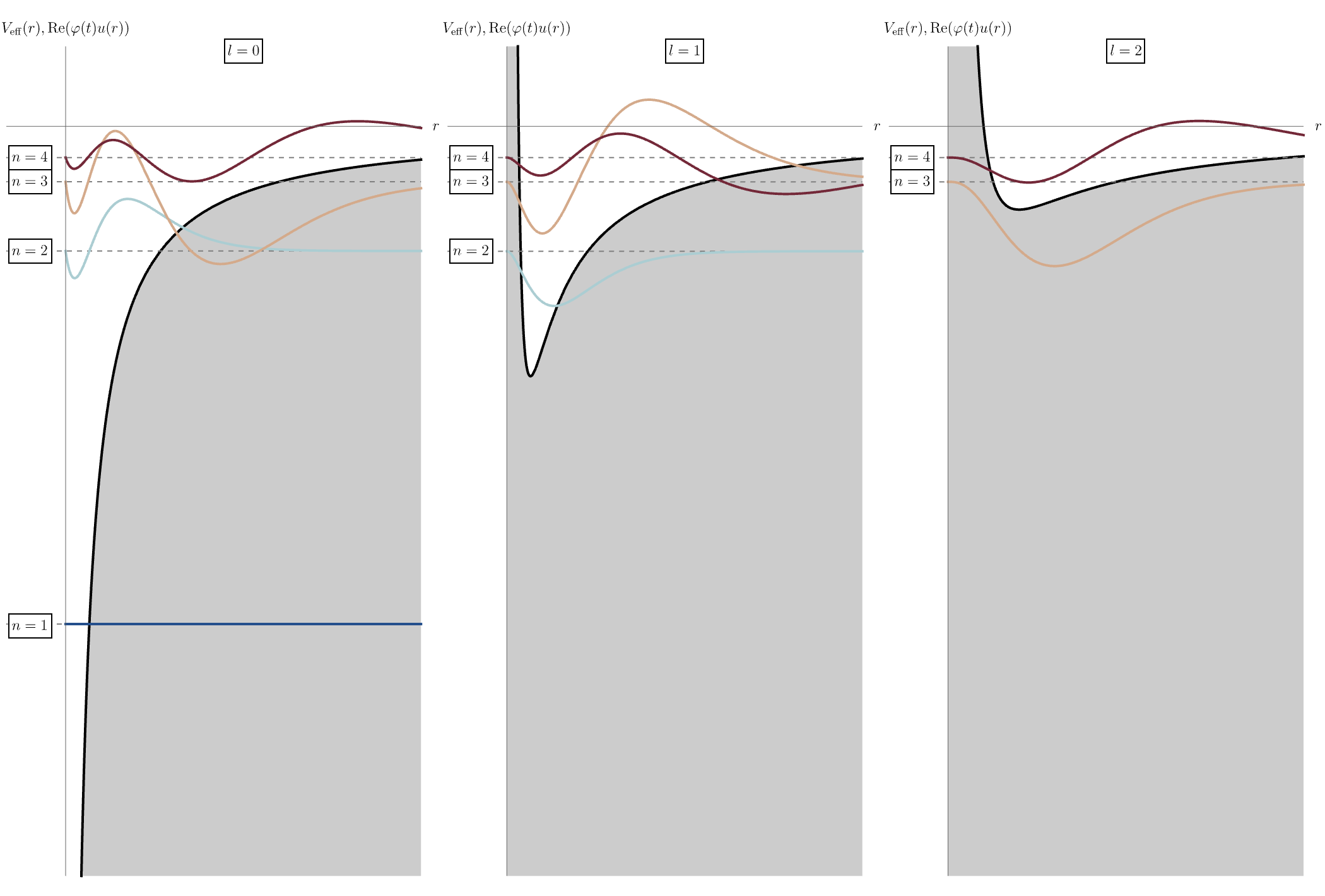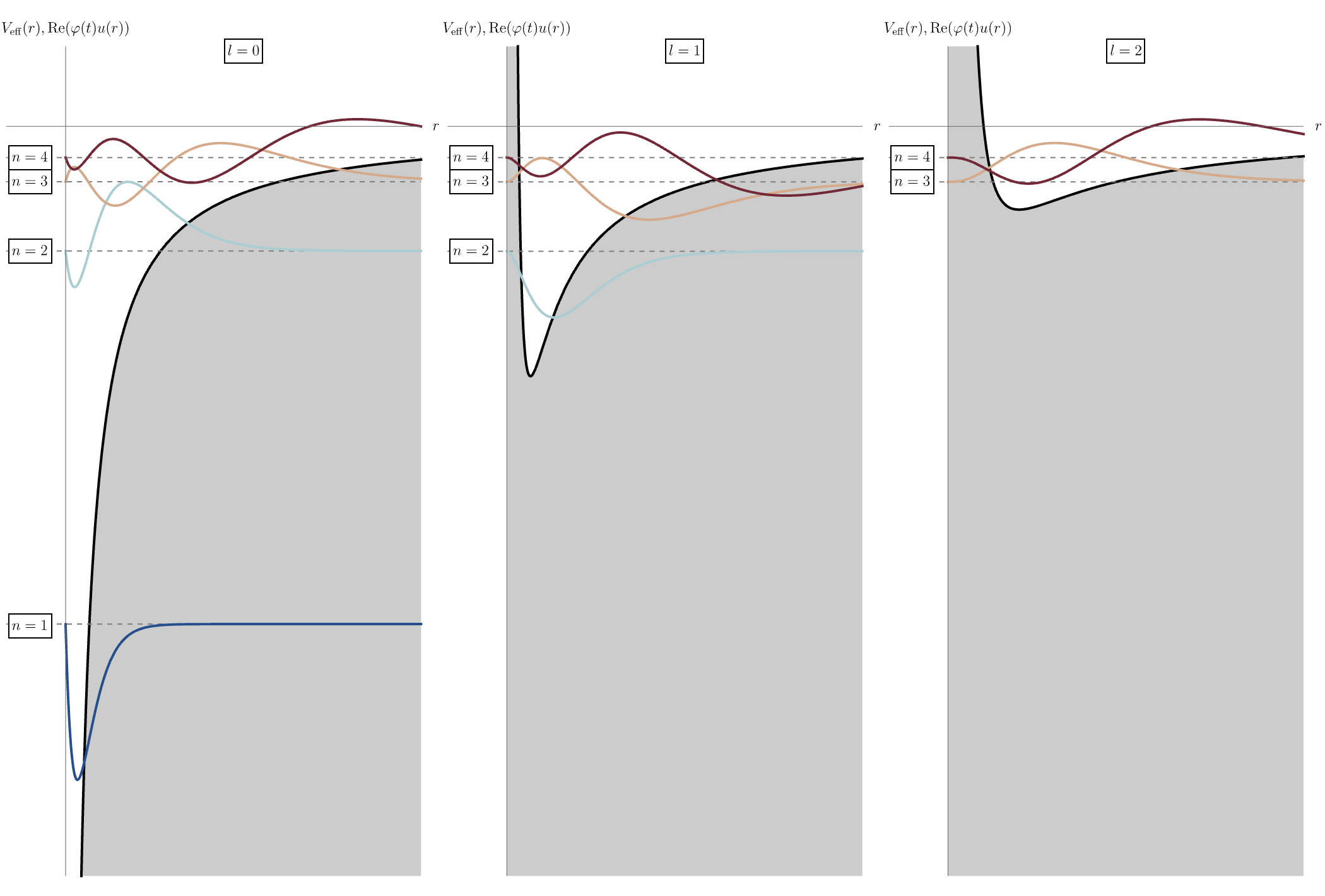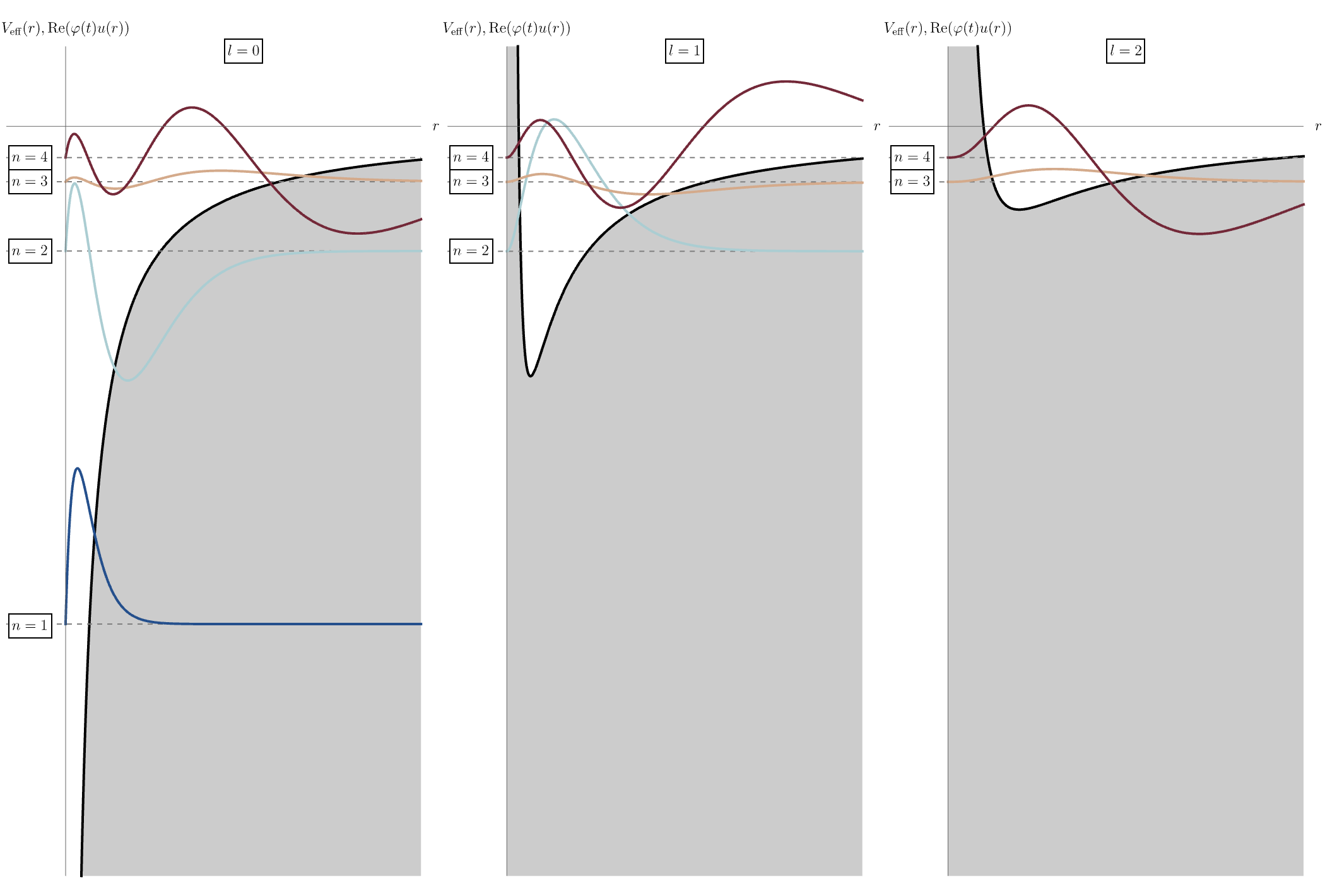
今回は水素原子の波動関数について学ぶ。 前回は、球対称なポテンシャル \( V (x, y, z) = V (r) \) に対しての時間に依存しない3次元Schrödinger方程式 \[ H \psi (x, y, z) = E \psi (x, y, z), \qquad H = - \frac{\hbar^2}{2 m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) + V (x, y, z), \] を \( \psi (x, y, z) = R (r) Y (\theta, \phi) \) と変数分離することで、動径方向 \( r \) と角度方向 \( \theta, \phi \) の方程式 \[ \frac{1}{R (r)} \frac{d}{d r} \left( r^2 \frac{d}{d r} R (r) \right) - \frac{2 m r^2}{\hbar^2} \left( V (r) - E \right) = l (l + 1), \] \[ \frac{1}{Y (\theta, \phi)} \left[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} Y (\theta, \phi) \right) + \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} Y (\theta, \phi) \right] = - l (l + 1), \] を導出した。 角度方向の解は球対称ポテンシャルの詳細に依らず球面調和関数として得られるのだった。 一方、動径方向の方程式はポテンシャルに依存する。 \( u (r) = r R (r) \) と置くと、方程式が1次元のSchrödinger方程式と似た形 \[ \frac{d^2}{d r^2} u (r) - \frac{2 m (V_{\rm eff} (r) - E)}{\hbar^2} u (r) = 0, \qquad V_{\rm eff} (r) = V (r) + \frac{\hbar^2}{2 m} \frac{l (l + 1)}{r^2}, \] になる。 ここに現れる \( V_{\rm eff} (r) \) は有効ポテンシャルと呼ばれ、2項目が遠心力によって中心へ近付きにくくなる効果を表している。 特に重要な水素原子 \[ V (r) = - \frac{e^2}{4 \pi \epsilon_0} \frac{1}{r}, \] の場合を考えよう。 下図の黒線は左から \( l = 0, 1, 2 \) に対する有効ポテンシャル \( V_{\rm eff} (r) \) を表している。 角運動量 \( l \) が大きくなるにつれて中心に近付きにくくなる様子がわかる。 また、\( V_{\rm eff} (r) \) の下での \( u (r) \) もアニメーションとして示されている。 水素原子のエネルギー準位 \( E_n \) は固有関数 \( u (r) = u_{n l} (r) \) を指定する \( n \) のみで決まり、 \[ E_n = \frac{E_1}{n^2}, \qquad E_1 = - \frac{m_e}{2 \hbar^2} \left( \frac{e^2}{4 \pi \epsilon_0} \right)^2 \simeq -13.6 \, {\rm eV}, \] となるため、下図では \( u (r) = u_{n l} (r) \) に \( \varphi (t) = \varphi_n (t) = e^{- i E_n t} \) を掛けた \( {\rm Re} (\varphi_n (t) u_{n l} (r)) \) を表示している。
最後に、前回求めた球面調和関数と合わせて、水素原子の波動関数 \[ \psi_{n l m} (r, \theta, \phi) = R_{n l} (r) Y_{l m} (\theta, \phi), \] の形を見てみよう。 下図の水平方向は角度部分を特徴付ける \( (l, m) \) (ただし \( m \geq 0 \) のみ表示) であり、垂直方向が動径部分を特徴付ける \( n \) である。 塗りつぶされた領域は波動関数の絶対値が一定以上の領域であり、色は波動関数の位相を示している。 中の様子が見えるように角度 \( - \frac{\pi}{2} < \phi < 0 \) の領域を切り取ってある。 また、図の上部に前回の球面調和関数 \( Y_{l m} (\theta, \phi) \) の形も表示してある。