Materials
1-1. 粒子の古典的振る舞いと量子的振る舞い
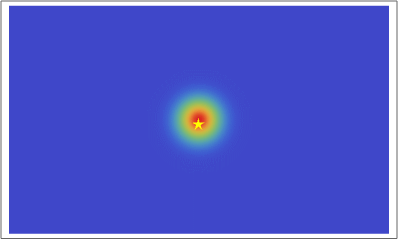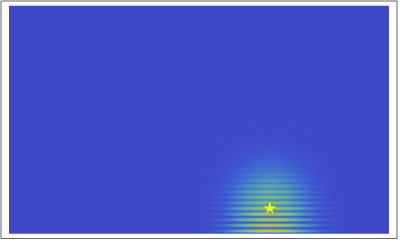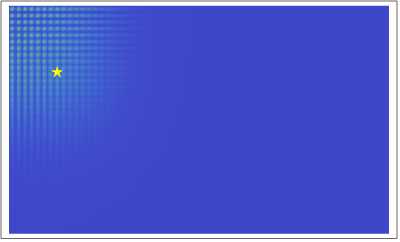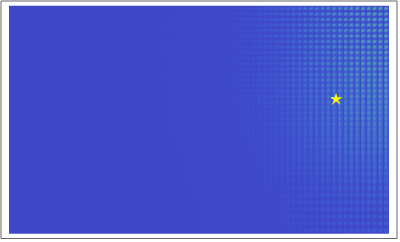
粒子の古典的振る舞いと量子的振る舞いを比べてみよう。
左図では粒子が壁からの撃力で跳ね返り、右図ではSchrödinger方程式
\[ i \hbar \frac{\partial}{\partial t} \Psi (t, x, y) = H \Psi (t, x, y), \qquad H = - \frac{\hbar^2}{2 m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right) + V (x, y) \]
にしたがって確率密度 \(\rho (t, x, y) = |\Psi (t, x, y)|^2\) が時間変化している。
どちらが「自然」に見えるだろうか?

1-2. 電子の干渉縞
スリットが2つある箱の中で、左から電子のビームを打ち込んだ様子。
図はそれぞれ波動関数の実部 \({\rm Re} \Psi (t, x, y)\)、波動関数の虚部 \({\rm Im} \Psi (t, x, y)\)、確率密度 \(\rho (t, x, y) = |\Psi (t, x, y)|^2\) である。
スリットより右側は強調のため色のスケールを100倍してある。
波動関数が箱の右端のスクリーン上に干渉縞を作り出している様子がわかるだろうか。
電子をこのスクリーン上で観測すると、観測確率に干渉縞が現れる。

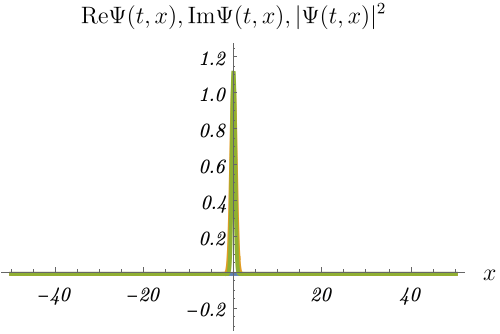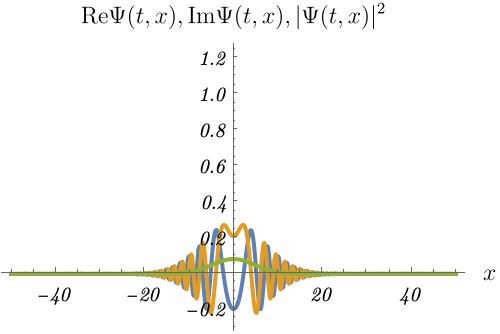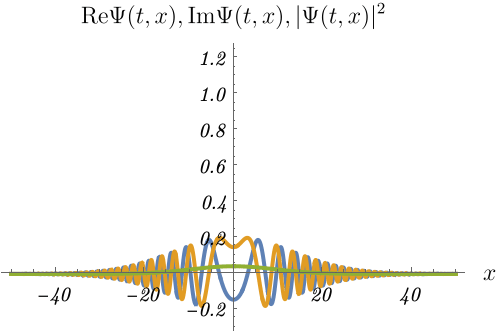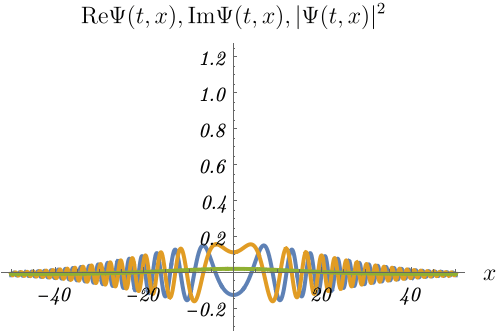
1-3. 粒子はどこに?
初期時刻で \(x = 0\) の位置に存在確率のピークがあったとしても、後の時刻では存在位置が広がってしまう。
図の青線・黄線・緑線は波動関数の実部 \({\rm Re} \Psi (t, x)\)・波動関数の虚部 \({\rm Im} \Psi (t, x)\)・確率密度 \(\rho (t, x) = |\Psi (t, x)|^2\) である。
確率密度の山が広がっていく様子が見えるだろうか。